Начать с того, что он не существует.
Вещественные числа можно рассматривать с разных сторон. Можно как алгебраическую конструкцию, с операциями сложить-умножить-поделить. А можно как топологическую конструкцию, которая имеет некоторую "непрерывность". Точнее, на правильном топологическом языке для множества говорят "полнота", а "непрерывность" - для функции из множества в множество.
Имея такое множество, можно по нему ходить, приближаясь к некоторой точке близко, ещё ближе, ещё ближе, и так далее. Это удобно, чтобы ввести понятие предела. Когда мы имеем просто множество, предел - это ещё скучно, ну дошли мы до 2, и дошли, а когда у нас есть функция, предел - это уже полезный инструмент. Можно найти предел
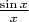
в точке 0.
Но нас не всё устраивает. Мы хотели бы брать не только такие пределы, а, чисто для целей исследования некоторых наших функций, хотели бы брать пределы, если стремиться в бесконечность - влево или вправо - и выразить как-то тот смысл, что сам предел получается бесконечный. И хотели бы делать это единообразно. Тогда мы вводим ещё одно поняти "близко, ещё ближе, ещё ближе" (ещё одну систему окрестностей), которые называем "окрестностями бесконечности", и
пополняем наше множество ещё одной точкой - к которой эти окрестности сходятся. Пополнение - это совершенно законная топологическая операция, например, она нужна, чтобы от множества рациональных чисел перейти ко множеству вещественных чисел (а без неё никак, можно вводить только разнообразные алгебраические).
При всём при этом наши операции сложения-умножения стояли в сторонке, забытые, и вот они обиделись: для новой точки

этих операций не определено. Если бы мы захотели их доопределить по непрерывности (как мы сделали с вещественными числами, честно говоря), то столкнулись бы с противоречиями: один предел, равный

даёт одно вещественное число, а другой - другое.
Кроме того, мы помним, что затеяли всё это для некоторых вполне конкретных функций, и будем постоянно натыкаться, что с другими функциями это не работает, или неудобно. Ситуация немножко лучше в комплексном анализе, но тоже не сахар. Поэтому к собственно вещественной прямой, которая и алгебраическая, и топологическая, элемент

не относят.
А в

-адических числах "бесконечностей" получается целый мешок...