Помогите пожалуйста разобраться со следующей задачкой:
"Записать выражение для плотности заряда с дипольным моментом
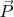
".
Как я делал: Помещаю отрицательный заряд в начало координат, записываю потенциал двух зарядов, пишу мультипольное разложение, в котором оставляю только член 1го порядка малости. Получается:

.
Далее,

.
Тогда

.
Нашел в задачнике Батыгина, Топтыгина похожую задачку (Гл.2, №99), но там ответ (точнее, нужное выражение выписано в условии) задачки совсем другое и вроде как не приводится к тому, что я получил...Подскажите, где я ошибся?