Решал задачу из Демидовича № 3652:
Найти экстремальные значения заданной неявно функции

от переменных

и

:

Я решал системой и нашел эти точки:
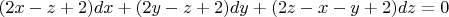
============================


![$\xymatrix{\ar@{=>}[r]&} x=y$ $\xymatrix{\ar@{=>}[r]&} x=y$](https://dxdy-04.korotkov.co.uk/f/3/a/1/3a1523b694a47f2c6204c8046f1448f182.png)

подставляем в уравнение:

============================
Решаем систему и находим

при


при

Подскажите как правильно определить точка (

или

) явл. точкой

или

?
Перепробовал кучу способов, но ответы так и не сошлись с ответом в задачнике.
Ответ в задачнике следующий:

точка

,

точка

.
Помогите пожалуйста!