Вы так же действовали для
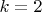
?
Для
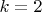
я в явном виде выписал многочлен

, принимающий значения

на числах

,

(имеются в виду единица с тройкой при сложении по модулю

) и

на остальных. И теперь, складывая числа

и

, я их вначале складываю побитовым ксором, а если

оказывается равным единице, то дополнительно ксорю

в старший разряд суммы.
При
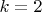
больше ничего делать и не надо, поскольку более старших разрядов у нас уже и нет. А вот при бОльшем

надо начинать учитывать дальнейшие переносы... Конечно, для каждого конкретного

можно тупо перебирать все возможные значения слагаемых и наворачивать многочлены, осуществляющие особое сложение для каждой их пары. Но это плохой метод: всё равно что составлять специальные таблицы умножения двухзначных, трёхзначных и т. д. чисел вместо того, чтобы учиться умножать столбиком. И длины формул будут экспоненциально разрастаться с ростом

. Хуже того, я даже не вижу систему, которое бы позволила однородным образом выписывать такие длинные формулы, просто замечаю, что раз

конечно, то там будет конечный перебор.
В идеале бы хотелось иметь одну и ту же формулу для всех достаточно больших

 -- Вс авг 26, 2012 01:51:16 --
-- Вс авг 26, 2012 01:51:16 --А ведь поразрядное умножение реализуется через выделение разряда! Выделяем, сдвигаем, умножаем, сдвигаем назад, а потом всё ксорим.
Я это мыслю так: храним в уме бит переноса, движемся справа налево, на очередной позиции ксорим два имеющихся разряда и бит переноса к ним до кучи, если проксорили не менее двух единиц, кладём в бит переноса

, иначе кладём

, сдвигаемся влево на следующую позицию и повторяем процедуру, останавливаемся, когда доходим до левого края.