Область определения (показательная функция и другие)

[Andrej-V]

Справочник по математике А.Г. Цыпкин, пункт "Рациональные алгебраические уравнения".
Автор пишет, что надо найти все корни числителя, все корни знаменателя, если числитель и знаменатель имеют один и тот же корень, то если степень этого корня у числителя больше, то этот корень является корнем рационального алгебраического уравнения. Прав ли он, или надо все корни знаменателя вычеркивать из области допустимых значений?
Подскажите пожалуйста область определения степенно-показательной ф-ии f1(x)^f2(x).
Часто пишется (-1)^n. Это какая функция? Входит ли в область определения показательной ф-ии требование неотрицательности основания?

[bot]

Andrej-V писал(а):

Справочник по математике А.Г. Цыпкин, пункт "Рациональные алгебраические уравнения".
Автор пишет, что надо найти все корни числителя, все корни знаменателя, если числитель и знаменатель имеют один и тот же корень, то если степень этого корня у числителя больше, то этот корень является корнем рационального алгебраического уравнения. Прав ли он, или надо все корни знаменателя вычеркивать из области допустимых значений?

Строго говоря - не прав. Однако в некоторых рассмотрениях может оказаться удобным заткнуть разрыв в такой точке, поскольку он устранимый. Так поступают во многих случаях - не только в случае рациональных функций.
С этой целью несколько изменяется определение, но это конечно требуется оговорить особо, как вообще всякое отступление от общепринятого.

Пример из алгебры:

Цитата:

На протяжении всей главы под кольцом будем разуметь ассоциативно-коммутативное кольцо с единицей и без делителей нуля.

[Andrej-V]

Спасибо.
Хочется все ж узнать область определения показательной и показательно-степенной ф-ии.
Входит ли а=1, где а - основание степени показательной ф-ии в ее область определения. Аналогично для показательно-степенной ф-ии f1(x)^f2(x), где f1(x) и f2(x) определены на всей числовой оси. Где-то встречал, что нужно f1(x) != 1; Чего-то сейчас не найду.
Вообще, что называется областью определения? Если это область в которой существуют значения ф-ии, то для показательной ф-ии область определения это не обязательно а > 0 (в таком случае м.б. и a < 0 , при некоторых заначениях х (в частности целых)). Вопрос здесь не в том, входит ли a < 0 в область определения, а в том, что такое область определения.

[Lion]

Andrej-V писал(а):

Подскажите пожалуйста область определения степенно-показательной ф-ии f1(x)^f2(x).
Часто пишется (-1)^n. Это какая функция? Входит ли в область определения показательной ф-ии требование неотрицательности основания?

Насчет первого вопроса где-то уже была активная дискуссия. В конце концов сошлись на том, что $f_1(x)>0$.
Если под функцией $(-1)^n$ Вы имеете в виду то, что пишется при решении тригонометрических уравнений, то это функция, определенная только на множестве целых чисел (или его подмножаствах). В область определения показательной функции обычно входит не только неотрицательность основания, но и то, что оно не равно 0.

[Andrej-V]

Я про (-1)^n имел в виду, что это показательная ф-я и следовательно основание д.б. >0 , несмотря на то, что n - целое.
Используется не только в тригонометрии, но и к примеру в вычислении определителей.
Все ж неясно a=1 входит или нет в область определения показательной ф-ии.

[Lion]

Некорректно рассматривать $(-1)^n$ как функцию при вычислениях (определителей, тригонометрии...), поскольку показательная функция должна быть определена на множестве положительных чисел. Обычно к этому добавляется ограничение, что основание не равно 1. Но, по-моему, если Вы будете рассматривать в качестве основания и 1, то ни к чему ужасному это не приведет.

[Andrej-V]

Обычно к этому добавляется ограничение, что основание не равно 1.
Я тоже так думал, но в тех учебниках, которые я просмотрел, (Смирнов, Фихтенгольц, Бергман, Кочетков) не написано, что в область определения не входит а=1. Там написано, что ф-я рассматривается при а ! = 1 (это написано, кажется, везде), при этом написано, что при а=1 ф-я - прямая линия. Кроме того во многих задачах из учебника Дорофеева, типа f1(x)^f2(x)=f3(x)^f4(x) ищется одно из решений f1(x)=1;f3(x)=1;
Не понятно, как должен считать абитуриент: может быть a=1?

[RIP]

Andrej-V писал(а):

Не понятно, как должен считать абитуриент: может быть a=1?

Может. Почему нет? Просто этот случай иногда надо рассматривать отдельно, как, например, в задаче $(x^2+0.5)^x=(x^2+0.5)^{1-x}$. (3 корня)

[Andrej-V]

RIP,
Я согласен.
Но и Lion написал:

Цитата:

Обычно к этому добавляется ограничение, что основание не равно 1.

Это ограничение - что такое, оно относится к О.О. или нет?

Цитата:

Может. Почему нет?

Но в такой логике задачка, похожая на Вашу имеет ли дополнительные корни (чтоб основания равнялись 0, а показатели нет): (x^2 - 0.5)^x = (x^2 - 0/5)^(1 - x)
Почему нет?
Я хочу найти четкую фразу: показательная ф-я определена при ...
Я такой фразы не нашел.

[RIP]

Andrej-V
Почитайте обсуждение в теме http://dxdy.ru/topic6332.html

[Andrej-V]

Уф. Прочитал.
Зачем посоветовали? Совсем запутался.
Вы там пишете, что рациональная (нецелая) степень от отрицательного числа определяется только для показателей вида +-1/n, где - нечетное натуральное число (например, n=3). Для всех остальных степень не определяется.
Откуда такое правило?
Бергмант, Араманович Краткий курс мат.анализа: Степенная ф-я определена для всех несократимых рациональных степеней p/q.
В Фихтенгольце, Смирнове и школьном учебнике Кочеткова Вашего правила нет.
А раньше я смеялся, когда Задорнов говорил, что в каком-то штате законодательно ввели чему должно быть равно Пи.

[незваный гость]

Andrej-V писал(а):

Уф. Прочитал.

Вы до конца почитайте. И не только RIP. Там подробно разбирается область определения $x^y$ и различных связанных функций (а также, почему она именно такова).

Andrej-V писал(а):

Бергмант, Араманович Краткий курс мат.анализа: Степенная ф-я определена для всех несократимых рациональных степеней p/q.

Это уже интересно. Чему равно $(-1)^{1/2}$? Или $1/2$ сократима?

Другой немаловажный вопрос: с какой точки зрения Вы ищите ответ? Школьный курс / вступительные экзамены? ТФКП? … Ответы могут оказаться разными…

Andrej-V писал(а):

А раньше я смеялся, когда Задорнов говорил, что в каком-то штате законодательно ввели чему должно быть равно Пи.

Ну, это известный авторитет. [off-topic]Между прочим, в США действует закон (примерно 1880х), что помидор — это овощ. Хотя всем известно, что с точки зрения биологической классификации он, как и арбуз — ягоды. Закон не устанавливает правила биологии, всего лишь таможенные правила. Другой пример: с точки зрения медицинского страхования США, беременность — это болезнь. Дальнейшее давайте в свободном полете, если конечно интересно.[/off-topic]

[Andrej-V]

незваный гость, я, конечно, поспешил. Хотел написать, что при х < 0 может существовать показатель, к примеру 3/5 (а не только с числителем дроби 1) У Бергмана, конечно, все расписано в виде таблички, где указан вид ф-ии в зависимости от значений p,q? где p - числитель в показателе, q - знаменатель.И, естественно, указано при q четном x>=0.
Про помидоры и арбуз. Они ягоды только потому, что ягодой называется ...., - они под это определение не попадают. И определение ягоды доминирует. Американцы не неправы. Просто они решили не делать такого определения ягоды, которое Вам нравиться. У них и неодушевленные предметы все среднего рода (хотя это не так с нашей колокольни).
Тему ту вчера прочитал до конца, но меня не интересует мнение каким должна быть О.О. Мы не в семинарии, где рассуждают о религиозных терминах, и каждый может сказать что-то свое, приближаясь к нирване. Число 3, кстати, тоже м.б. написано в виде 6/2, но не в этом суть. Суть в том, что не написано в учебниках: 1. Определение области определения. 2.Сами области определения тоже написаны нечетко. Пример - те же дроби в числителе. Здесь не надо рассуждать. Здесь надо, чтоб было правило.

[RIP]

Andrej-V писал(а):

Вы там пишете, что рациональная (нецелая) степень от отрицательного числа определяется только для показателей вида +-1/n, где - нечетное натуральное число (например, n=3). Для всех остальных степень не определяется.
Откуда такое правило?

Такие ограничения были у нас в курсе мат. анализа. Именно так, только с 1 в числителе. Вроде бы я видел такое же соглашение в каком-то учебнике по мат. анализу, но точно не помню. Лично я склонен соглашаться с этим правилом. Если говорить строго, то имеется в виду следующее. Функция $f(x)=x^a$ в зависимости от постоянной $a$ имеет следующую область определения:
1) если $a\in\mathbb{N}\cup\{0\}\cup\{\frac1n\mid n~-\text{ натуральное нечётное}\}$, то $x\in\mathbb{R}$ (причём $x^0=1$ при $x\in\mathbb{R}$);
2) если $a\in\{-n\mid n\in\mathbb{N}\}\cup\{-\frac1n\mid n~-\text{ натуральное нечётное}\}$, то $x\in\mathbb{R}\setminus\{0\}$;
3) при всех остальных $a$: $x\geqslant0$ или $x>0$, если $a>0$ или $a<0$ соответственно.

Но возникает проблема, когда мы рассматриваем такие выражения, как $x^{\frac{-2}{-6}}$ или $x^{\frac{\sqrt3}{\sqrt3}}$. Если рассматривать их как частные случаи функции $f(x)=x^a$, то они определены при $x\in(-\infty;+\infty)$. Но когда вместо $x$ стоит конкретное число, то дело усложняется. Согласитесь, что равенства $(-8)^{\frac{-2}{-6}}=-2$ и $(-1)^{\frac{\sqrt3}{\sqrt3}}=-1$ смотрятся несколько дико. Поэтому удобно в таких случаях считать, что $x>0$, поскольку для положительных $x$ проблем не возникает.


По поводу области определения (моя точка зрения):
Область определения функции --- множество, на котором эта функция определена, как ни банально это звучит. Но дело в том, что задать функцию --- это не просто написать какую-то формулу и сказать, что вот это мол и есть наша функция (хотя в задачах обычно так и делают). Задание области определения входит в определение фукции, если подходить к этому делу строго.

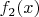
Просто когда функцию задают с помощью выражения, то вид этого выражения "по умолчанию" задаёт и область определения с помощью некоторых правил типа такого: если в выражение входит $f_1(x)^{f_2(x)}$ с непостоянной функцией $f_2(x)$, то автоматически в О.О. входит неравенство $f_1(x)>0$ (некорректная фраза, т.к. в ОО входит не само неравенство, но смысл понятен), и не потому, что при других $x$ выражение не определено, а просто потому, что это неравенство входит в ОО.

P.S. Повторюсь, что это лишь моя точка зрения на предмет. Она может не совпадать с "официальной".

[Lion]

RIP писал(а):

Задание области определения входит в определение фукции, если подходить к этому делу строго.

Если подходить еще строже, то нужно заметить, что $f\colon V\to W$ и $f\colon U\to W$, где $U\subset V$ --- разные (!!!) функции.