Parallel transport along a closed loop is a test of presence of curvature which is created by deficit angle.
That is only when you consider a 2-dimensional manifold. When you have more dimensions, you can test what will become a vector that is initially pointing perpendicular to the loop's tangent plane. And it can also be skewed some way in the end. Maybe in some fourth orthogonal direction, if this is allowed by the dimension nubmer.
Riemann tensor has 4 indexes: 2 lower have to do with a plane; upper with a vector that we are transporting; last one with a tangent vector, I guess.
Last one shows where the initial vector will be skewed to after a trip.
On the contrary, Ricci Tensor is a more complicated story. An idea, how can volume deviate is very unclear.
Ok, look at some curved 2-dimensional surface. You can not only transport vectors along it, you can also measure areas. And if you take the Gaussian curvature, you will find that these things are related to each other. Namely, you can mark a small 'cap' on the surface, selecting some center point, and stepping some fixed distance from it in every direction. Then you can calculate two measures of curvature:
1. ratio of the circumference of the 'cap' to its radius;
2. ratio of the area of the 'cap' to the square of its raduis.
Sure, both numbers won't be equal to
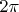
and
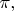
and sure, they will approach those values in a limit
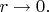
But the difference to a limit value, divided by an appropriate power of
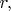
will approach to some fixed non-zero number, and this number will be the Gaussian curvature,
in both cases. This means, whatever is done to the surface in terms of lengths, the same happens in terms of surface measure. When you raise dimensions, you will talk about volume intead of area, but the idea will be the same.
-- 25.07.2012 01:53:23 --Basically, it says that how gravitational potential varies all over the place is some constant (4piG) times the density? Look, here I have the same kind of confusion.
Ok, we should go back to the idea of a
field source. There are many field equations that have structure
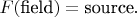
Maybe it's early to study GR if you are not familiar with other examples of (physical) fields. The Poisson Equation is an archetype case. Now remember how it works in electrostatics: there are some 'field lines' represented mathematically as a vector field
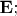
the lines are related to the potential by
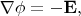
and to the charges by
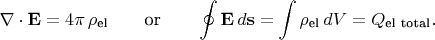
The last equation is most important: it says that lines never break and never end, unless thes come from some charge, or go into some negative charge. By analogy to the flow of fluid, these points, where lines 'flow out' or 'flow in', are called the
sources and
drains of the vector field. Or shortly, just sources (positive or negative).
When you established the picture with sources and vector field lines, we can think of the potential again. Imagine some 2-dimensional plane, then the scalar potential
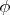
could be viewed as some 'lanscape' over it - a surface specified by the function
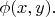
On this surface there can be slopes and plains, hills and cavities, mountains and mountain passes. All these features somehow correspond to the picture of lines. What we are interested in are
second derivatives - features that look like humps and hollows when dissected by a vertical plane. There are three kinds of those: a hill, a cavity, a saddle. Now, when we are in space between charges, the second derivative of
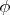
is zero, so the landscape can have a shape only of plains, slopes and saddles. And when we are inside some charged space, say in the uniformly charged ball, the shape of the landscape can be a hill (if the charge density is positive) or a cavity (if negavive).
So that is what the source is in the thery of fields: it is the point where something external influences the field, something interacts with it, and then the field cannot be uniform in that point. If the equation refers to the heat transport, then sources are where the heat is extracted. If the equation refers to the wave propagation, then sources are points (or regions) of wave radiation. And so on. Regarding gravitation, the sources should be attracting masses, which make the field be pulling any test body in their direction. In the (gravitational now) Poisson's equation, attracting masses make cavities in the landscape, and around these cavities there should be slopes, because the lanscape cannot immediately become flat again without violation of the Poisson's Equation. And those slopes make test bodies roll down, towards the attracting masses, exactly what we wanted out mathematical model to show.