Вот ответ, привожу в техе, поскольку он очень здоровый и на экран не влезает:
Код:
f \left( x \right) ={\it \_C1}\,{\it HeunG} \left( -1,-1/4\,{\frac {
\left( c+m\sqrt {4+c+a-b} \right) \sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,
\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}+m \left( -
4+c+a+b-2\,\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }
\right) }{\sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,\sqrt {- \left( -1+m
\right) ^{2} \left( a+b+c-4 \right) }}}},1/2+1/4\,\sqrt {4+c+a-b}+1/2
\,m+1/4\,\sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,\sqrt {- \left( -1+m
\right) ^{2} \left( a+b+c-4 \right) }},-1/4\,{\frac { \left( -2\,m-
\sqrt {4+c+a-b}-2 \right) \sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,\sqrt {-
\left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}+c+a+b-8\,m+4\,{m}^
{2}}{\sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,\sqrt {- \left( -1+m \right) ^{
2} \left( a+b+c-4 \right) }}}},m,1+1/2\,\sqrt {4+c+a-b},-x \right)
\left( -x-1 \right) ^{1/2+1/4\,\sqrt {4+c+a-b}} \left( -x+1 \right) ^
{-1/4\,{\frac {-2\,\sqrt { \left( -4+4\,m \right) \sqrt {-a-b-c+4}+8-8
\,m-c-a-b+4\,{m}^{2}}+ \left( 2-2\,m \right) \sqrt {-a-b-c+4}+a+b+c-4}
{\sqrt { \left( -4+4\,m \right) \sqrt {-a-b-c+4}+8-8\,m-c-a-b+4\,{m}^{
2}}}}}+{\it \_C2}\,{\it HeunG} \left( -1,1/4\,{\frac { \left( \left(
-2+m \right) \sqrt {4+c+a-b}-c \right) \sqrt {8-8\,m-c-a-b+4\,{m}^{2}+
4\,\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}+
\left( -2+m \right) \left( -4+c+a+b-2\,\sqrt {- \left( -1+m \right)
^{2} \left( a+b+c-4 \right) } \right) }{\sqrt {8-8\,m-c-a-b+4\,{m}^{2}
+4\,\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}}},3/2+
1/4\,\sqrt {4+c+a-b}-1/2\,m+1/4\,\sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,
\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }},-1/4\,{
\frac { \left( -6-\sqrt {4+c+a-b}+2\,m \right) \sqrt {8-8\,m-c-a-b+4\,
{m}^{2}+4\,\sqrt {- \left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}
+c+a+b-8\,m+4\,{m}^{2}}{\sqrt {8-8\,m-c-a-b+4\,{m}^{2}+4\,\sqrt {-
\left( -1+m \right) ^{2} \left( a+b+c-4 \right) }}}},-m+2,1+1/2\,
\sqrt {4+c+a-b},-x \right) {x}^{1-m} \left( -x-1 \right) ^{1/2+1/4\,
\sqrt {4+c+a-b}} \left( -x+1 \right) ^{-1/4\,{\frac {-2\,\sqrt {
\left( -4+4\,m \right) \sqrt {-a-b-c+4}+8-8\,m-c-a-b+4\,{m}^{2}}+
\left( 2-2\,m \right) \sqrt {-a-b-c+4}+a+b+c-4}{\sqrt { \left( -4+4\,
m \right) \sqrt {-a-b-c+4}+8-8\,m-c-a-b+4\,{m}^{2}}}}}
Цитата:
The HeunG function is the solution of the Heun General equation. Following the first reference (at the end), the equation and the conditions at the origin satisfied by HeunG are
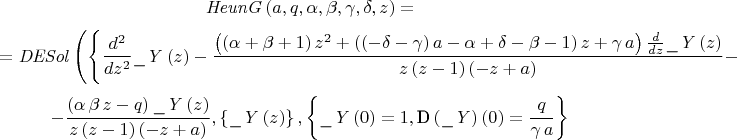
Heun's equation is an extension of the 2F1 hypergeometric equation in that it is a second-order Fuchsian equation with four regular singular points. The 2F1 equation has three regular singularities. The HeunG function, thus, contains as particular cases all the functions of the hypergeometric 2F1 class.
Из общего хелпа:
Цитата:
The five multiparameter Heun equations have been popping up with surprising frequency in applications during the last 15 years. Heun equations include as particular cases the Lame, Mathieu, spheroidal wave, hypergeometric, and with them most of the known equations of mathematical physics.
Five Heun functions are defined as the solutions to each of these five Heun equations, computed as power series solutions around the origin satisfying prescribed initial conditions.
[1] Decarreau, A.; Dumont-Lepage, M.C.; Maroni, P.; Robert, A.; and Ronveaux, A. "Formes Canoniques de Equations confluentes de l'equation de Heun." Annales de la Societe Scientifique de Bruxelles, Vol. I-II. (1978): 53-78.
[2] Ronveaux, A., ed. Heun's Differential Equations. Oxford, England: Oxford University Press, 1995.
[3] Slavyanov, S.Y., and Lay W. Special Functions, A Unified Theory Based on Singularities. Oxford, England: Oxford Mathematical Monographs, 2000.