Это проблема, которая интересовала меня очень давно. Простых реккурентных формул для коэффициэнтов разложения функции в ряд здесь быть не может. Конечно же, существует функциональный произвол на множестве
непрерывных решений этого уравнения, даваемых методом, указанным
neo66. Это я знал. Действительно, достаточно определить на отрезке

, таком что

монотонно строго возрастающую функцию

, такую что

,

и

для

, а дальше она задается на всей действительной оси.
Можно ограничиться заданием всего одной промежуточной точки

, а затем рассмотреть поржденные ею промежуточные точки

расположенные между точками

Я пробовал, правда это было очень давно, с калькулятором в руках и на бумаге (Мапла тогда еще тоже не было) брать различные значения

и экстраполировать эскизно график такой функции по этим промежуточным точкам, но у меня всегда получалась функция с иррегулярным поведением - волнистым, то есть ее производные уже не являются монотонно возрастающими, как у экспоненты - все это меня очень огорчало.
Даже если потребовать любую степень гладкости, все равно функциональный произвол остается. Но вот если потребовать аналитичность функции...
Я опять же давно проделывал это уже на Мапле, но условия, налагаемые на коэффициэнты ряда получаются непотребными даже для численного их нахождения. Я усекал функцию до многочленов, ограничиваясь конечным числом младших членов ряда Тейлора. Аналитичность в точке сшивки задавал условиями:

.
Но Мапл отказывался искать численое решение коэффициэнтов выше некоторого их числа. Потом, заменив

на

(для упрощения) и рассмотрев корни полученных многочленов, с ростом их степени (и ростом их приближения к точному решению), увидел, что корни почти равномерно заполняют некую приближенную окружность, радиус которой, к тому же, сужается. При увеличении степени, корни на "окружности" будут сгущаться. Получается, что точное аналитическое решение будет определено в области малого радиуса комплексной плоскости и за нее аналитически непродолжаемо?! Это будет печальный факт.
Но это устаревшие результаты. Вот что получил только что на Мапле, но уже через интерполяцию по одной произвольной точке

. Этот метод гораздо проще, но имеет ограничение. Взял

точек интерполяции (

больше

брать нельзя - сверх большие числа) при
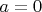
и

(это точка

из очень узкого интервала, сравнимого с погрешностью, где при

все коэффициэнты Тейлора выходят положительными), что дало полином Лагранжа степени 7:
0.43306619*10^{-10}*t^7+
0.33642825*10^{-8}*t^6+
0.15984091*10^{-4}*t^5+
0.35242958*10^{-3}*t^4+
0.22010205*10^{-1}*t^3+
0.24978246*t^2+
0.87564105*t+
0.49858060
В интервале

погрешность между

и

не превышает 10%.
Возможно, при

точки

, при которых все коэффициэнты Тейлора положительны, будут

.
Меня конечно заинтересовала и более общая задача: найти решение

и

(где обязательно

). Тогда, очевидно, что

и

, а

- решение первоначальной задачи при

. То есть, это обобщение операции композиции одинаковых функций на нецелые кратности

которое, конечно, будет иметь смысл лишь если оно вводиться единственным образом.
Для просто непрерывных решений имеет место все тот же функциональный произвол, но что будет для аналитических функций по

и

? Существует ли такое решение, да притом только с положительными коэффициэнтами ряда Тейлора по

(все производные по

монотонно возрастают при любых

).
Ведь единственно же решение

и

при целых

. Это проблема единственности построения аналитической функции, заданной на счетном дискретном множестве и дополнительно всюду удовлетворяющей некоторому функциональному соотношению.
Потом, проанализировав задачу, я понял, что есть и еще более общая и естественная постановка этой задачи. Пусть на замкнутом интервале

- конечном, полубесконечном или бесконечном, задана некая функция

, такая, что

,

,

при

и

при

. Функция

на интервале

принадлежит определенному классу: дифференцируема

раз (при

- локально интегрируема по Ньютону, что верно для монотонных функций), непрерывно дифференцируема

раз (при

- непрерывна), бесконечно дифференцируема, либо аналитична. Существует ли функция

, заданная при

и

, такая что:

и

(то есть

), притом

имеет тот же класс (или выше) по

что и

при любом

и аналитична по

при любом

и

? Единственна ли она?
То есть, достаточны ли предложенные условия, налагаемые на функцию

, для обобщения операции композиции данной функции от самой себя на нецелые кратности

.
При фиксированном

значения функции по

также монотонно возрастают и пробегают весь интервал

.
Если нет требования

(что может быть для конечных

), то

не определена при целых

для достаточно больших

, а если не требовать

, то

не определена при целых

для достаточно малых

. Если же и

и

, то

не определена при целых

достаточно больших по модулю. И тогда бессмыслено искать аналитическое продолжение на любые

.
Это конечно совсем не олимпиадная задача, даже

не олимпиадная.
Если
кто-нибудь, хоть
что-нибудь знает о постановке данной проблемы или даже решении этого удивительного математического феномена!...