знакомы вы с ТФКП (теория функции комплексного переменного)?
Был такой предмет на 2-ом курсе, но я его подзабыл

. Вот пытаюсь разобраться.
Под

будем подразумевать значение с

.

Надо показать, что

Поскольку функция

всюду аналитична, интеграл от нее по замкнутому контуру равен нулю:

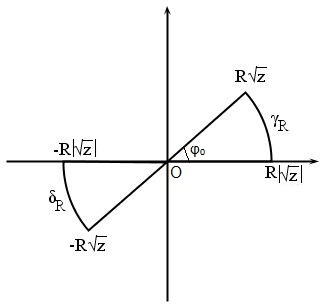
Т.к. на дуге

можно положить
![$u=Re^{i\phi},\ \phi\in[0,\phi_0]$ $u=Re^{i\phi},\ \phi\in[0,\phi_0]$](https://dxdy-02.korotkov.co.uk/f/5/4/b/54b6bad714a764a3300e6b5668d8769082.png)
, имеем

и, следовательно,

при

(т.к.

).
С учетом

переходя в

к пределу при

, получим

.
Есть ли ошибки?