I'm too lazy to work out a good solution... We can assume that
![$S=[-1,1]^2$ $S=[-1,1]^2$](https://dxdy-02.korotkov.co.uk/f/9/c/5/9c5165951e5ff44822d1dad54c9a503e82.png)
and
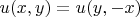
(otherwise take the symmetrisation of it; the "mean-value" fact for the initial function will follow easily from the one for the symmetrised function). Denote

the harmonic conjugate of

(Of course,

. Integrate
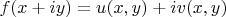
along the contour consisting of diagonal

going from
![$[-1,-1]$ $[-1,-1]$](https://dxdy-03.korotkov.co.uk/f/e/a/d/eadb0c26637799849cb755e836de3e4482.png)
to
![$[1,1]$ $[1,1]$](https://dxdy-03.korotkov.co.uk/f/a/8/d/a8da069a976ad42b72a37dda354a139882.png)
, side

going from
![$[1,1]$ $[1,1]$](https://dxdy-03.korotkov.co.uk/f/a/8/d/a8da069a976ad42b72a37dda354a139882.png)
to
![$[1,-1]$ $[1,-1]$](https://dxdy-02.korotkov.co.uk/f/1/2/7/127510c6b95bb846f327a78b2c75539282.png)
and side
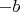
going from
![$[1,-1]$ $[1,-1]$](https://dxdy-02.korotkov.co.uk/f/1/2/7/127510c6b95bb846f327a78b2c75539282.png)
to
![$[-1,-1]$ $[-1,-1]$](https://dxdy-03.korotkov.co.uk/f/e/a/d/eadb0c26637799849cb755e836de3e4482.png)
. (Let
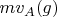
denote the mean value of a function

on a line

.) We obtain
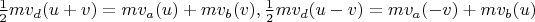
, now add these and use that

(because

is analytic). I think I wrote too much for this problem. I should stop here.