Масса всего шара: оболочки и воздуха внутри неё равна

.
И пусть температура всего (оболочки,воздуха внутри неё, стены и окр. среды ) в начале равна
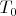
, если она конечно понадобится.Да, ещё также даны модули упругости: шара -

,стены -

и коэффициенты Пуассона шара -

,стены -

.
Так это Вы сами задачу составляете?
Если сами, то можете из этой задачки сделать три.
1.Про воздушный шарик с массой воздуха m и пренебрежимо малой массой оболочки. Ее Вы уже решили- кинетическая энергия перешла во внутреннюю энергию газа. Процесс можно считать адиабатическим, поскольку удар непродолжителен по времени.
2.Про воздушный шарик с воздухом массой m1 и массой тонкой оболочки m2. Решение посложнее, если часть исходной кинетической энергии перейдет в энергию упругой деформации оболочки.
3.Задачка про сплошной резиновый шарик, ударяющийся о жесткую стенку. Это задача Герца.