Tuzembobel писал(а):
Здравствуйте! Такая задачка: доказать, что все корни уравнения

вещественные.
У функции

особые точки - только полюса в точках

. Во-первых, докажем ограниченность тангенса вне некоторой окрестности полюсов, т.е. функция

ограничена в

, где

- замкнутый круг радиуса

с центром в точке

.
Т.к.

, то достаточно доказать ограниченность

в нашей области

.
Пользуясь периодичностью косинуса, достаточно доказать ограниченностю косинуса для

.
Но

.
Следовательно, функция

ограничена в

и для

выполняется

на границе круга радиуса

; Тогда можно применить теорему Руше для области

:

Но в вывод кажется странным, т.к., по-моему, это уравнние имеет более чем одно (нулевое) решение
Во-первых, оценка

на границе области

сделана неверно (как минимум, она должна зависеть от

и стремиться к бесконечности при

). Вы не учли, что границы кругов

также являются частью границы области

.
Во-вторых, вывод не кажется странным, так как остальные корни уравнения

(кроме корня

) попадают как раз внутрь тех самых "маленьких кружочков"

.
Добавлено спустя 15 минут 12 секунд:
RIP
На самом деле теорема Руше здесь применима, но не "в лоб".
Действительно, можно показать, что если

- это контур, состоящий из отрезков прямых

,

(т.е. квадрат со стороной

и центром в нуле), то на этом контуре

.
Поэтому при любом натуральном

выполняется

.
Но сразу теперь применять теорему Руше нельзя, поскольку функция

не аналитична внутри контура

. Однако если мы напишем следствие этого неравенства:

, то теперь теорему Руше можно смело применять, т.к. обе функции теперь уже аналитичны внутри

. Тогда получим, что уравнение

имеет столько же корней внутри контура, сколько и уравнение

(столько же решений будет иметь и уравнение

), а именно

штук.
Для завершения доказательства того, что все корни уравнения

вещественны, осталось лишь заметить, что уравнение

тоже имеет

корней на отрезке
![$[-\pi n,\pi n]$ $[-\pi n,\pi n]$](https://dxdy-01.korotkov.co.uk/f/4/3/0/430ce53ac9e9c6455fb9a6e87236328882.png)
(с учетом кратности: корень

имеет кратность 3, остальные
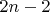
корней имеют кратность 1). Это можно посмотреть, например, по рисунку.