What is your personal opinion about the inequality mentioned?
Если Вы имеете в виду Ваше предыдущее неравенство, то я его доказал с помощью метода
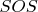
. После нескольких довольно грубых оценок. Получилось очень громоздко, что говорит о том, что оно очень нестрогое. Простое доказательство, правда, не нашёл и поэтому своё громоздкое доказательство публиковать не хочу.
Если Вы имеете в виду неравенство из этого топика, то на вид оно ещё более громоздкое и поэтому лень мучиться ещё раз. Это всё имхо, конечно. Может, существует что-то красивое, а я это не вижу.
Yes, it is the same person... and I believe when he have more time he will give an answer.
Это за полтора-то года! Правда, для того чтобы сказать, что неравенство доказывается с помощью Мюрхеда, хватило и двух дней... Как-то это всё некрасиво выглядит, имхо.