Единственность решения системы из двух нелинейных уравнений

[Nimza]

Рассмотрим систему из двух уравнений на пару чисел $x,y > 0$

$$ \begin{array}{rcl} g(x,y) & = & \gamma, \\ g(\alpha x,\beta y) & = & \gamma \end{array} $$

Гладкая функция $g(x,y)$ вогнута и положительно однородна первой степени при $x,y>0$; $\alpha, \beta, \gamma > 0$ --параметры, $\alpha, \beta \neq 1$, $\alpha \neq \beta$. Доказать, что если система имеет решение, то оно единственно.

(Оффтоп)

Например, если $g(x,y)$ -- линейная функция, то система запишется в виде

$$ \begin{array}{rcl} Ax+By = \gamma, \\ (A\alpha)x + (B\beta)y = \gamma \end{array} $$

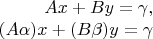
Понятно, что для такой системы это верно.

Другой пример подходящей функции: $g(x,y) = ( x^{-n} + y^{-n} )^{-\frac{1}{n}}$, где $n = 1,2,\ldots$.