Преобразование Лапласа как переход к новому базису

[mclaudt]

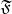
Хочется выстроить прикладную схему взаимосвязи между преобразованиями Фурье $\mathfrak{F}$ и Лапласа $\mathfrak{L}$. Речь о самом общем случае непрерывного преобразования Фурье (нормировка опущена) $\mathfrak{F}\{f\}=F(\omega) = \int_{\mathbb R} e^{-i\omega t}f(t)dt$ и двусторонним преобразованием Лапласа $\mathfrak{L}\{f\}=F(s) = \int_{\mathbb R} e^{-st}f(t)dt$.

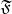
$\mathfrak{F}$ - это переход к новому базису в пространстве комплекснозначных функций вещественного аргумента с интегрируемым квадратом. Преобразование унитарно, поэтому фактически новый базис просто повернут по сравнению со старым (из дельта-функций).

Основные упоминаемые рецепты интерпретации Лапласа таковы:

• $\mathfrak{L}$ - это тоже вроде "поворот" (точнее, поворот со сколом и потерей ортогональности, т.н. skewed, из-за неунитарности $\mathfrak{L}$).
• Некий аналог Фурье, но с комплексными частотами, с заменой вещественной переменной $t$ на $it$, т.е. то, что именуется Wick rotation и имеет аналогии в связи уравнения диффузии и уравнения Шредингера переходом к комплексному времени.
• Также упомянуто, что $F(\omega)$, будучи аналитически продолженным на $\mathbb C$, даст $F(s)$.

Два вопроса:
1. О каком пространстве функций идет речь, если трактовать Лапласа как поворот базиса со сколом?
2. Нельзя ли как-то обобщить Лапласа, чтобы он использовал интегрирование по всей области определения - $\mathbb C$, (как и Фурье - по $\mathbb R$)? Откуда такой выбор контуров интегрирования в Лапласе? Нельзя ли определить в общем виде что-то вроде $F(s) = \int_{\mathbb C} e^{-su}f(u)du$, где $f(u)$ - аналитическое продолжение $f(t)$ на $\mathbb C$? Чтобы двойственность Понтрягина была видна и в случае в Лапласом, и интеграл брался бы по всей плоскости, а не только по прямой на ней?

[mclaudt]

Вот релевантные ссылки по теме, но ни одна из них не проливает свет окончательно.

http://mathoverflow.net/questions/383/m ... ition/2141
http://www.physicsforums.com/showthread.php?t=155709
http://mathoverflow.net/questions/2809/ ... transforms
http://math.stackexchange.com/questions ... or-dummies
http://forums.xkcd.com/viewtopic.php?f=17&t=62999
http://www.reddit.com/r/math/comments/e ... _transform

Все "прозревшие" восторженно ссылаются на лекцию дедка из MIT, который показал, что есть общего между разложением в ряд по степеням и разложением по базису экспонент - т.е. разложение по базису путем скалярного произведения. Но это-то банально вроде, а вот дальше обобщений никто не просит.

[g______d]

По поводу первого вопроса: давайте определимся с уровнем строгости. Выше было про какой-то базис из дельта-функций --- что это такое?

Можно предположить, что вопрос состоит в том, относительно какой нормы преобразование Лапласа можно считать унитарным.

Насчет второго вопроса --- я не понимаю мотивации. Чем интеграл по всему $\mathbb C$ будет лучше? Начнем с того, что класс функций, продолжающихся на $\mathbb C$, значительно уже, чем область определения преобразования Лапласа.

[mclaudt]

Спасибо за интерес к теме.

g______d в сообщении #548360 писал(а):

Выше было про какой-то базис из дельта-функций --- что это такое?

Обобщение базиса $\{1, 0, 0, ... , 0 \}, \{0, 1, 0, 0, ... , 0 \}, ... , \{ 0, 0, ... , 0, 1\}$ на бесконечномерное пространство функций f(t), т.е. когда дискретный индекс заменили непрерывным параметром. Не уверен насчет подводных камней.

g______d в сообщении #548360 писал(а):

Можно предположить, что вопрос состоит в том, относительно какой нормы преобразование Лапласа можно считать унитарным.

Так, или же, скорее, "что это за базисные функции, какого пространства, на которые проецируется оригинал при преобразовании Лапласа".

g______d в сообщении #548360 писал(а):

ем интеграл по всему $\mathbb C$ будет лучше?

Например, тем, что в формулировке преобразования будет использована вся область определения преобразуемых функций, как и в случае преобразования Фурье.
Наверняка, такой выбор пути интегрирования является следствием сведения интеграла по $\mathbb C$ к интегралу по контуру.

[g______d]

mclaudt в сообщении #548369 писал(а):

Обобщение базиса $\{1, 0, 0, ... , 0 \}, \{0, 1, 0, 0, ... , 0 \}, ... , \{ 0, 0, ... , 0, 1\}$ на бесконечномерное пространство функций f(t), т.е. когда дискретный индекс заменили непрерывным параметром. Не уверен насчет подводных камней.

Они появятся, когда Вы попытаетесь придумать строгое определение базиса. Например, его элементы не будут принадлежать самому пространству (т. к. дельта-функция ни при каком разумном определении не интегрируема с квадратом).

mclaudt в сообщении #548369 писал(а):

Например, тем, что в формулировке преобразования будет использована вся область определения преобразуемых функций, как и в случае преобразования Фурье.

Не понял. Как в преобразовании Фурье, так и в преобразовании Лапласа область определения функций --- это $\mathbb R$. Откуда взялось $\mathbb C$? Вот, например, есть у вас функция Хевисайда (равная 0 при $x<0$ и 1 при $x\ge 0$). Одна из самых простых функций, для которых определено преобразование Лапласа. Как ее расширять на $\mathbb C$? У нее нет даже непрерывного продолжения, не то что аналитического.

[mclaudt]

g______d в сообщении #548376 писал(а):

Например, его элементы не будут принадлежать самому пространству

Комплексные экспоненты тоже не интегрируемы по квадрату, но по ним раскладываются функции, которые по квадрату интегрируемы. Юриспруденция аксиоматики базиса - вещь, далекая от конструктивной юзабельности.

g______d в сообщении #548376 писал(а):

Как в преобразовании Фурье, так и в преобразовании Лапласа область определения функций --- это $\mathbb R$

Да, просто если рассматривать Лапласа как поворот/скол базиса, в каком-то пространстве, то, так как образ - функция комплексной переменной, то и исходную функцию по идее тоже хочется рассматривать как функцию комплексной переменной, и искать общую формулировку преобразования Лапласа функций комплексной переменной, которая бы использовала скалярное произведение по всей комплексной области.

[g______d]

mclaudt в сообщении #548395 писал(а):

Комплексные экспоненты тоже не интегрируемы по квадрату, но по ним раскладываются функции, которые по квадрату интегрируемы. Юриспруденция аксиоматики базиса - вещь, далекая от конструктивной юзабельности.

Ну это все-таки математический форум. Понятно, что Вы можете интерпретировать преобразование Фурье в $L_2$ как "разложение по экспонентам", а запись $f(x)$ как "разложение по $\delta$-функциям", но это физический уровень строгости, причем примерно 50-летней давности. И на таком уровне строгости легко запутаться, какие вещи можно делать с этим базисом, а какие нет. Если хочется математического ответа, то надо переформулировать вопрос на математическом языке. Например, в терминах унитарных операторов.

mclaudt в сообщении #548395 писал(а):

образ - функция комплексной переменной

И часто ли она продолжается на все $\mathbb C$?

[mclaudt]

g______d в сообщении #548400 писал(а):

И часто ли она продолжается на все $\mathbb C$?

Знать бы, что принципиального в аналитичности образа, можно было бы и ответить. В Фурье вон раскладываются произвольные функции действительной переменной, и образ может быть разрывен, и даже обобщенной функцией.

g______d в сообщении #548400 писал(а):

50-летней давности

Ланжевен оперировал стохастической силой, не дожидаясь, пока математики разработают юридические нормы для стохастических дифуров. И интуитивный смысл их не изменился и через сотню лет. Не думаю, чтобы интуиция скалярного произведения и ортогональности кардинально мутировала за полвека.

В любом случае, интересует лаконичное и утилитарное обобщение преобразования Лапласа, в терминах базисных функций.

-- Ср мар 14, 2012 22:44:28 --

g______d в сообщении #548400 писал(а):

Если хочется математического ответа,

Хочется конструктивного ответа, в стиле Арнольда. Парсить же дамп законодательной базы по функциональным пространствам лучше специализированными ATP-программами.

[g______d]

mclaudt в сообщении #548408 писал(а):

Знать бы, что принципиального в аналитичности образа, можно было бы и ответить.

В любом случае область определения образа преобразования Лапласа --- далеко не всё $\mathbb C$. И оно зависит от исходной функции. Например, преобразование Лапласа от функции Хевисайда определено только в правой полуплоскости. Как Вы его будете продолжать в левую? Вы же хотите потом что-то делать по всему $\mathbb C$.

mclaudt в сообщении #548408 писал(а):

В Фурье вон раскладываются произвольные функции действительной переменной, и образ может быть разрывен, и даже обобщенной функцией.

Разложите мне функцию $e^{e^x}$.

[mclaudt]

g______d в сообщении #548417 писал(а):

Разложите мне функцию $e^{e^x}$.

Впечатлило бы, но вообще-то я осведомлен про интегрируемость квадрата, и указал её в самом начале. Речь о том, что никаких требований на непрерывность, и уж тем более аналитичность, на аргумент преобразования Фурье не накладывается, и мне хочется узнать, нет ли подобного же всеядного обобщения операции поворота базиса на функции комплексного аргумента, коим может привидеться преобразование Лапласа несчастным с изувеченной конструктивизмом психикой.

-- Ср мар 14, 2012 23:34:17 --

g______d в сообщении #548417 писал(а):

Например, преобразование Лапласа от функции Хевисайда определено только в правой полуплоскости. Как Вы его будете продолжать в левую?

А если ввести аналогичное требование конечности нормы функции? Хотя вся надежда на 50 лет развития функана, может, они обрисуют картину правильно. Не хочется искать черный велосипед в темной комнате.

[g______d]

mclaudt в сообщении #548422 писал(а):

Впечатлило бы, но вообще-то я осведомлен про интегрируемость квадрата, и указал её в самом начале.

Ок, просто если есть интегрируемость квадрата, то обобщенных функций не будет, а Вы о них говорили.

mclaudt в сообщении #548422 писал(а):

А если ввести аналогичное требование конечности нормы функции?

Уже лучше; можно придумать такую норму, чтобы преобразование Лапласа было целой функцией (например, суммируемость со сверхэкспоненциальным весом).

Тем не менее, я по-прежнему не понимаю изначального вопроса. Пусть Вам дана функция на вещественной оси, от которой мы хотим вычислять преобразование Лапласа. Вы предлагаете переписать его в виде интеграла по $\mathbb C$. Для этого надо существенно расширить область определения исходной функции. Если это хочется сделать с помощью аналитического продолжения, то не слишком ли это сильное требование --- существование продолжения на всю плоскость? Если продолжение производится каким-то другим способом, то возникает вопрос о том, почему мы выбрали именно такое продолжение и единственно ли оно.

[mclaudt]

g______d в сообщении #548448 писал(а):

Ок, просто если есть интегрируемость квадрата, то обобщенных функций не будет, а Вы о них говорили.

А, согласен, это я вспомнил про плоскую волну и её Фурье-образ в виде дельта-функции. Но сами плоские волны-то в пространство не входят...

g______d в сообщении #548448 писал(а):

Вы предлагаете переписать его в виде интеграла по $\mathbb C$.

Я не настаиваю, мне лишь хочется, как это сделано для Фурье, видеть в преобразовании Лапласа умножение вектора-функции на матрицу перехода, которая состоит из координат нового базиса в старом базисе, по всем правилам линейной алгебры. И так как конечный вектор имеет комплексные индексы, то и начальный, будучи вектором того же пространства (раз у нас поворот координат со сколом), должен быть комплекснозначной функцией комплексного аргумента.