Сумма целых частей кубических корней

[Ktina]

Для каждого натурального $m>1$ найти все натуральные $n$ такие, что $\lfloor \sqrt[3] 1\rfloor+\lfloor \sqrt[3] 2\rfloor+\dots +\lfloor \sqrt[3] n\rfloor=mn$

(Оффтоп)

Если придумывая эту задачу, я ничего не напутала, получается очень красивая последовательность, которой, кстати, нет в OEIS.

[hippie]

При $m=1:\quad n\in\{1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7\}.$

При $m>1:\quad n=\frac{\left(\frac{k^2+k}2\right)^2-k}{k-m},$ где $k=\left[\sqrt[3]n\right].$

Компьютерная проверка показала, что такие $n$ существуют при $m\in\{1,\ 2,\ 7\}$ и при $m$ кратных трём.

[hippie]

Вот список $n<10000000,$ соответствующих целым $m.$

$m=1,\qquad n=1;$
$m=1,\qquad n=2;$
$m=1,\qquad n=3;$
$m=1,\qquad n=4;$
$m=1,\qquad n=5;$
$m=1,\qquad n=6;$
$m=1,\qquad n=7;$
$m=2,\qquad n=33;$
$m=3,\qquad n=96;$
$m=6,\qquad n=644;$
$m=7,\qquad n=1005;$
$m=9,\qquad n=2024;$
$m=12,\qquad n=4620;$
$m=15,\qquad n=8816;$
$m=18,\qquad n=14996;$
$m=21,\qquad n=23544;$
$m=24,\qquad n=34844;$
$m=27,\qquad n=49280;$
$m=30,\qquad n=67236;$
$m=33,\qquad n=89096;$
$m=36,\qquad n=115244;$
$m=39,\qquad n=146064;$
$m=42,\qquad n=181940;$
$m=45,\qquad n=223256;$
$m=48,\qquad n=270396;$
$m=51,\qquad n=323744;$
$m=54,\qquad n=383684;$
$m=57,\qquad n=450600;$
$m=60,\qquad n=524876;$
$m=63,\qquad n=606896;$
$m=66,\qquad n=697044;$
$m=69,\qquad n=795704;$
$m=72,\qquad n=903260;$
$m=75,\qquad n=1020096;$
$m=78,\qquad n=1146596;$
$m=81,\qquad n=1283144;$
$m=84,\qquad n=1430124;$
$m=87,\qquad n=1587920;$
$m=90,\qquad n=1756916;$
$m=93,\qquad n=1937496;$
$m=96,\qquad n=2130044;$
$m=99,\qquad n=2334944;$
$m=102,\qquad n=2552580;$
$m=105,\qquad n=2783336;$
$m=108,\qquad n=3027596;$
$m=111,\qquad n=3285744;$
$m=114,\qquad n=3558164;$
$m=117,\qquad n=3845240;$
$m=120,\qquad n=4147356;$
$m=123,\qquad n=4464896;$
$m=126,\qquad n=4798244;$
$m=129,\qquad n=5147784;$
$m=132,\qquad n=5513900;$
$m=135,\qquad n=5896976;$
$m=138,\qquad n=6297396;$
$m=141,\qquad n=6715544;$
$m=144,\qquad n=7151804;$
$m=147,\qquad n=7606560;$
$m=150,\qquad n=8080196;$
$m=153,\qquad n=8573096;$
$m=156,\qquad n=9085644;$
$m=159,\qquad n=9618224.$

[nnosipov]

hippie, если $m=3l$, то $n=64l^3+32l^2+4l-4$. Кажется, соответствует Вашей таблице.

И для таких $m$ это единственное значение $n$.

[Dave]

Если $k=\lfloor \sqrt[3] n\rfloor$, то имеем формулу:

$$n=\frac {k(k-1)(k^2+3k+4)} {4(k-m)}, \eqno(1)$$

где $k^3 \leqslant n < (k+1)^3$, откуда при $k>1$:

$$k-1 < \frac {k(k-1)(k^2+3k+4)} {(k+1)^3} < 4(k-m) \leqslant \frac {(k-1)(k^2+3k+4)} {k^2} < k+3.$$

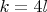
При достаточно больших $k$ дробь $(1)$ может давать целое число только если $4(k-m)=k$. Случаи, когда знаменатель равен $k+1$ или $k+2$ нетрудно перебрать отдельно. Значит, по большому счёту, $3k=4m$ и $m=3l$, $k=4l$ при любом натуральном $l$, откуда находим вышеуказанную формулу для $n$.

[nnosipov]

Что-то в этом духе и у меня получилось, правда, подлиннее.

[Dave]

Самый "нетривиальный" случай - $m=7, \; n=1005, \; (k=10)$. Кроме него есть только $m=2, \; n=33, \; (k=3)$.

(Оффтоп)

33, наверное, означает 33-й зуб Кстати, помните шутку про $3/8$ зуба?

Я бы сформулировал задачу так: какие целые значения может принимать среднее

$$\frac {\lfloor \sqrt[3] 1\rfloor+\lfloor \sqrt[3] 2\rfloor+\dots +\lfloor \sqrt[3] n\rfloor} n \quad \text{?}$$

[nnosipov]

Dave в сообщении #547516 писал(а):

(Оффтоп)

33, наверное, означает 33-й зуб Кстати, помните шутку про $3/8$ зуба?

Я бы сформулировал задачу так: какие целые значения может принимать среднее

$$\frac {\lfloor \sqrt[3] 1\rfloor+\lfloor \sqrt[3] 2\rfloor+\dots +\lfloor \sqrt[3] n\rfloor} n \quad \text{?}$$

(Оффтоп)

А что за шутка? Что-то не припоминается. Но в любом случае задача удалась, с чем можно ТС и поздравить.

[Dave]

nnosipov в сообщении #547520 писал(а):

(Оффтоп)

А что за шутка? Что-то не припоминается.

(Оффтоп)

Рассказ врача стоматологической клиники.

Мой один хороший знакомый (с математическо-програмистским уклоном) привез свою знакомую ко мне лечиться. Работа была довольно обширная, все надо было сделать как можно быстрее. После полуторачасовой работы я вывожу довольную пациентку и говорю такие слова " Леш... Ты, пожалуйста, доставь ее домой и пусть она вечером мне позвонит (я буду волноваться) Я удалил ей три восьмых зуба.." Вижу в глазах моего приятеля гамму чувств и начинаю его понимать. Он воспринял мои слова как дробное число.
1. Т.е. если я удалил 3/8 зуба ,то на хрена я оставил 5/8.
2. Это каким же надо быть мастером, чтобы так зубы удалять?
3. И чего я там ковырялся полтора часа?