Критерий Фишера ,критерий F как вы говорите, имеет вид:

, где

- это дисперсия адекватности.

, где

- это расчетные значения вашей величины, полученные по вашей модели, а

- это значения, измеренные вами,

- это количество степеней свободы, вычисляемое по формуле, имеющей вид:

,где

- число коэффициентов уравнения, N - число опытов в матрице планирования.
Дисперсия вопроизводимости:

, где

- это дисперсия в каждой строке, где вы проводили параллельные эксперименты (у вас 5 параллельных экспериментов), вид её формулы:

, где

-это значения вашей величины в каждом u-ом параллельном опыте для i-го измерения

,

- это число параллельных опытов.
После того как вычислите
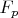
, его надо сравнить с

и если

, то модель адекватна. Для

нужно знать

и

.