Скатывающийся с горки заряженный шар

[Omega]

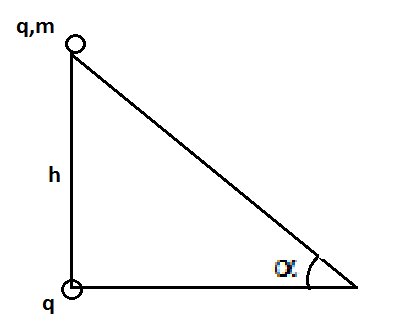
Всем привет. Проверьте решение вот такой задачки:
С неподвижной горки высотой $h$ и углом наклона $\alpha$,в основании которой находится неподвижный заряд $q$, скатывается маленький, имеющий такой же заряд, шарик массой $ m$...Найдите скорость шарика в конце скатывания,пренебрегая его размерами и силой трения.

Итак по ЗСЭ: $mgh+W_{{1}}=\frac {m{v}^{2}}{2}+W_{{2}}$. Где $W_{{1}}={\frac {k{q}^{2}}{h}}$ - энергия электростатического поля в верхней части горки, а $W_{{2}}={\frac {k{q}^{2}\tg \left( \alpha \right) }{h}}$ - в её низу.Тогда для $v$ получаем: $v=\sqrt {2\,gh+2\,{\frac {k{q}^{2} \left( 1- {\it tg} \left( \alpha\right) \right) }{mh}}}$.
Насчёт ответа не уверен. Думаю попробовать более сложным путём - через работу силы Кулона.Что-то типа:

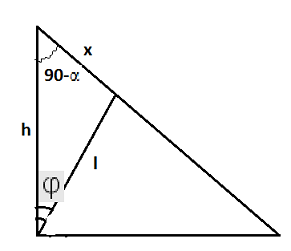
По теореме синусов имеем ${\frac {{\it dx}}{d\varphi }}={\frac {l}{\cos \left( \alpha \right) }}$ для $ \varphi \rightarrow 0$ или же ${\frac {{\it x}}{sin(\varphi) }}={\frac {l}{\cos \left( \alpha \right) }}$.Используя это и теорему косинусов получаем , что $l_{{1}}={\frac {h\cos \left( \alpha \right) }{\cos \left( \alpha- \varphi \right) }}$ или $l_{{2}}={\frac {h\cos \left( \alpha \right) }{\cos \left( \alpha+ \varphi \right) }}$, однако так как $\varphi \in [0;\pi/2]$ исключим второй ответ.Полная работа силы Кулона во время скатывания шарика равна

$$A=\int\limits_{0}^{h/\sin \left( \alpha \right)}} \frac{k{q}^{2}}{{l}^{2}}} dx=\int\limits_{0}^{\alpha} \frac{-k{q}^{2} }{{l \cos(\alpha)}} } d\varphi + \int\limits_{\alpha}^{\pi/2} \frac{k{q}^{2} }{{l \cos(\alpha)}} } d\varphi = \int\limits_{0}^{\alpha} \frac{-k{q}^{2} \cos (\alpha-\varphi) }{{h \cos^{2}(\alpha)}} } d\varphi + \int\limits_{\alpha}^{\pi/2} \frac{k{q}^{2} \cos (\alpha-\varphi) }{{h \cos^{2}(\alpha)}}}d\varphi=$$

$$={\frac {k{q}^{2} \left( \cos \left( \alpha\right) \right-\sin \left( \alpha \right))}{h\cos^{2} \left( \alpha \right) }}$$

Не знаю правильно ли я перешёл от $dx$ к $d\varphi$ и правильно ли вообще я нашёл работу.И того в итоге получаем $ v=\sqrt {2\,{\it gh}+2\,{\frac {k{q}^{2} (1-\left \tg \left(\alpha\right) \righ) }{mh \left \cos\left(\alpha \right) \right }}}$.
В принципе не сильно отличается).Откуда же этот косинус лишний или не лишний). Что не верно?

[ewert]

(Оффтоп)

неправильно прочитал картинку

[obar]

Через закон сохранения энергии правильно. Только лучше говорить не про скатывание, а про соскальзывание (при скатывании надо учитывать момент инерции).

[ewert]

obar в сообщении #539808 писал(а):

Только лучше говорить не про скатывание, а про соскальзывание

Это-то как раз не очень принципиально -- надо будет просто добавить поправочный множитель. Кстати, условие сформулировано неаккуратно -- непонятно, имелось ли в виду скатывание или соскальзывание: слова "скатывается" и "трением пренебречь" формально противоречат друг другу.

Но интереснее поставить другой вопрос: при каком угле постановка задачи вообще некорректна, т.е. шарик просто не сможет прокатиться (ну или проскользить) вдоль всей плоскости?...

[Omega]

Да,простите,соскальзывает.

[Munin]

ewert в сообщении #539828 писал(а):

Но интереснее поставить другой вопрос: при каком угле постановка задачи вообще некорректна, т.е. шарик просто не сможет прокатиться (ну или проскользить) вдоль всей плоскости?...

$\alpha<\tfrac{\pi}{4}$

[ewert]

Munin в сообщении #539851 писал(а):

$\alpha<\tfrac{\pi}{4}$

Нет, конечно. Рассмотрите предельный случай, когда заряд очень маленький.

[Bulinator]

ewert в сообщении #539828 писал(а):

Но интереснее поставить другой вопрос: при каком угле постановка задачи вообще некорректна, т.е. шарик просто не сможет прокатиться (ну или проскользить) вдоль всей плоскости?

$\alpha<\alpha_0=\arccos{\sqrt[3]{\frac{q^2}{mgh^2}}}$

[obar]

Это с чего вдруг? Заряды ведь одноименные. Движению ничего не мешает. Формально ответ верен при всех углах, даже если шарик отрывается от плоскости (лишь бы не пролетел основание).

[Oleg Zubelevich]

а еще можно кривую скорешего спуска поискать

[ewert]

obar в сообщении #539916 писал(а):

Формально ответ верен при всех углах, даже если шарик отрывается от плоскости

Вот то-то и оно. Отрыв -- это уже и не скатывание, и не скольжение, да и бог весть где он после отрыва приземлится. Если даже на саму плоскость -- поди пойми, куда он отскочит. А если он не на плоскости, а нанизан на проволочку, то и тут не слава богу -- его можно тогда и запереть. В любом варианте неаккуратная формулировка.

[Omega]

Я точно не помню условие, однако там было сказано: считайте, что шарик не отрывается от горки.
Так откуда же этот косинус во втором ответе? Кто-нибудь проверьте решение.