По индукции. Рассмотрим любой набор

, для которого

Тогда

Замена
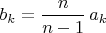
даёт

По индукционному предположению оба утверждения верны для набора

и, следовательно, и для набора

. А в силу произвольности нумерации -- и для всего набора

, ч.т.д. (база индукции при

достаточно очевидна).