Здравствуйте, я снова со своими тараканами...
Задача: Пусть
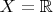
, а

состоит из пустого множества и дополнений всевозможных конечных подмножеств прямой

. Является ли

топологией?
Я бы ответил - нет. Но в решении указано, что является. Более того, носит даже специальное название "топологии Зариского"...
Тут мне несколько неясно:
а) имеются ли в виду "дополнения конечных подмножеств прямой" или "всевозможные конечные подмножества прямой"?
б) дополнение конечного подмножества в

- бесконечно? Или я что-то не так понимаю?
в) утверждая, что

- топология мне не удается даже доказать первой аксиомы! Не могу понять как
бесконечное объединение всевозможных конечных подмножеств в

может быть конечным? Конечное объединение конечных множеств - понимаю... Но тут не тот случай, или я не прав?
г) была задача, в которой нужно было в

привести пример пересечения двух бесконечных множеств, которое является конечным. Я привел такой:
![$(-\infty; a] \cap [a; +\infty) = \left{ a \right}$ $(-\infty; a] \cap [a; +\infty) = \left{ a \right}$](https://dxdy-01.korotkov.co.uk/f/8/a/9/8a9f04403a899b5e0a21a1ef219640f082.png)
(в смысле точки, или одноэлементного множества, как угодно). Непонятно, однако, является ли примером следующий вариант:

? Насколько я понимаю, любой сколь угодно малый интервал в

- бесконечное множество!
Проясните, пожалуйста, ситуацию!