Руководство по XY-pic для пользователя с навыками программирования
- очень мощная штука, но одновременно сложная и невнятно описанная, что препятствует её более широкому использованию. С помощью
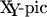
можно рисовать не только коммутативные диаграммы (а вы это часто делаете?), но и почти любые рисунки, которые вы готовы набросать на доске. Примеры кода рисунков на
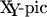
часто выглядят абракадаброй. Между тем, это идейно очень простая штука.
Этим полукреслом я попытаюсь изложить, что сам понял (и в процессе понимания), для себя и для окружающих, для свободного и непринуждённого повседневного использования  на форуме, в общем случае. Для узкозаточенных частных случаев могут быть свои приёмы. Если здесь чего-то не хватает, смотрите [RM] и [RMS].Используемая нотация
на форуме, в общем случае. Для узкозаточенных частных случаев могут быть свои приёмы. Если здесь чего-то не хватает, смотрите [RM] и [RMS].Используемая нотация при описании синтаксиса (неформальном):
<$%.?ляляля - терминальные символы, буквально те, которые надо писать
<название> - нетерминальные символы, которые надо заполнять по смыслу
{ } - необязательная часть
... - повторение
% пояснения до конца строки - комментарий LaTeX в примерах, игнорируется
Иногда одни и те же конструкции даны в тексте в нескольких вариантах: более простом и более универсальном. Большинство конструкций упрощены по сравнению с полными возможностями, полные варианты см. в [RM].
Основной источник:
[RM] Kristoffer H. Rose, Ross Moore, Xy-pic Reference Manualhttp://ctan.uni-altai.ru/macros/generic ... yrefer.pdfТакже использовался
[RMS] Kristoffer H. Rose, Ross Moore, Xy-pic Complete Sources with TeXnical Commentaryhttp://mirror.macomnet.net/pub/CTAN/mac ... source.pdfкоторый представляет собой [RM], перемежающийся с

-исходниками
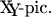
Для тех, кому неинтересно это занудство, есть другие замечательные руководства:
Circiter, Руководство по использованию XY-pic на форумеtopic35475.htmlSomeone, Коммутативные диаграммыpost169421.html#p169421Они частично базируются на документе
Kristoffer H. Rose, Xy-pic User's Guidehttp://mirror.macomnet.net/pub/CTAN/mac ... yguide.pdfТехническое замечание: из того, что перечислено в разделах II и III в [RM], на форуме доступны
\usepackage[matrix,arrow,curve,frame,poly,arc]{xy}
(сообщение администратора:
post340588.html#p340588 ). Именно они и перечислены у меня в разделе 4. Соответственно, другие опции (описанные в разделах II и III в [RM]) на форуме недоступны. Или их можно попросить у администрации, как это сделал
Circiter.
1. Стандартное обрамление.
1.1 Задание ориентации и масштаба системы координат
2. Как подготовить рисунок к его рисованию в XY-pic
3. Как XY-pic рисует рисунок (ядро)
3.1. Как перемещаться по рисунку
3.2. Как создавать объекты
3.3. Как размещать объекты
3.4. Как создавать текстовые метки
3.5. Как создавать линии
3.6. Как именовать положения
3.7. Как перемещаться по рисунку - продвинутые способы
3.8. Как модифицировать объекты - продвинутые способы
post544572.html#p5445724. Готовые объекты (features)
4.1. Кружки и рамки
4.2. Стрелки
4.3. Правильные многоугольники (полигоны)
4.4. Матрицы
4.5. Окружности, эллипсы, дуги
4.6. Кривые по многим точкам
5. Программирование для XY-pic
6. Справочные материалы
6.1. Стрелки
6.2. Кончики стрелок
6.2. Рамки
7. Пример по шагам
Пример 1: Перемещение по рисунку и "сброс" объектов. - п. 3.2.
Пример 2: Объекты и текстовые метки. - п. 3.4.
Пример 3: Линии. - п. 3.5.
Пример 4: Плоский график. - п. 3.5.
Пример 5: Стереометрический рисунок. - п. 3.5.
Пример k: Графики функций (нарисованные приблизительно, "от руки"). - п. 4.6.
1. Стандартное обрамление.Рисунок XY-pic вставляется на форуме следующим образом:
[math]$$\begin{xy} /r1cm/:, <команды XY-pic> ... \end{xy}$$[/math]
Теги
[math] удобно писать явно, чтобы можно было делать переносы строк - обычно XY-рисунок - текст большой. Пробелы можно не ставить, как всегда.
Пустых строк оставлять нельзя. Ставить
$$ или
$ можно по желанию: в одном случае рисунок будет выделен в отдельный абзац и расположен по центру, а в другом - включён в строку, как и обычная формула. Можно ставить комментарии LaTeX: от символа
% до конца строки.
1.1 Задание ориентации и масштаба системы координатКусочек
/r1cm/:, - это, на самом деле, первая команда XY-pic, её удобно ставить, чтобы задать масштаб, в котором вы будете рисовать рисунок. Её формат:
/ <буква направления> <величина длины для LaTeX> /:,
По сути, она задаёт ориентацию системы координат на холсте, и длину, которая будет дальше считаться за 1. По умолчанию устанавливается правая система координат, с масштабом 1 = 1 мм.
<
Буква направления> бывает
r,
u,
l,
d, и указывает направление оси

: вправо, вверх, влево, вниз. Ось

откладывается от

перпендикулярно против часовой стрелки (как на обычных математических графиках) и имеет тот же масштаб. Вот как будет ориентирован единичный вектор по

для разных <
букв направлений> (надпись расположена в
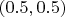
):

<
Величина длины для LaTeX> состоит из числа (с десятичной точкой или без неё) и единицы длины LaTeX. Напомню, в LaTeX есть такие единицы длины:
pt, dd, bp (point, didot point, big point) - типографский пункт, около 0,35 мм
pc, cc (pica, cicero) - 12 пунктов, примерно высота шрифта
in - дюйм, примерно 6 пика
mm - миллиметр
cm - сантиметр
em - ширина буквы M текущего шрифта
ex - высота буквы x текущего шрифта
mu - 1/18 ширины буквы M текущего математического шрифта, 1/3 пробела \,
Разумеется, это всё будет нарисовано в виде картинки на форуме, и изображено на мониторе, так что
1cm вряд ли точно окажется 1 см.
2. Как подготовить рисунок к его рисованию в XY-picНабросайте эскиз на бумаге (включая текстовые метки). Прикиньте координаты объектов, последовательность их рисования, возможные имена объектов, разметьте эскиз соответственно. Если используются кривые линии - прикиньте расположение их управляющих точек. Будьте готовы к отладке рисунка, или к постепенному его собиранию из более простых элементов.
3. Как XY-pic рисует рисунок (ядро)XY-pic - это целый язык внутри языка, имеющий рекурсивную грамматику. Рисунок - это последовательность <
команд XY-pic> (в [RM] - <
pos>, fig. 1 p. 8), каждая из которых может иметь сложный синтаксис, и в частности, содержать другие последовательности <
команд XY-pic>. Команды обозначаются символами, что придаёт XY-pic компактность и трудночитаемость. Фигурные скобки
{ } нельзя свободно использовать для группировки, как в LaTeX.
Основа логики рисования в XY-pic - пошаговое управление положением рисовательного инструмента, типа "черепашки". Её можно перемещать, рисовать в текущем положении простые графические элементы (объекты), запоминать её положения под разными именами, и возвращать в именованное положение. Даже если не работать с именами, для черепашки всегда доступны её текущее положение
current, c и предыдущее
previous, p. Два положения надо помнить, чтобы проводить стрелочки от одной точки к другой (и вообще разнообразные линии). Также задана аффинная система координат
base, в которой интерпретируются координаты точек (см. 3.1). Изменяя эту систему координат, можно совершать аффинные преобразования над целыми рисунками.
Проще всего пользоваться такими способами управления "черепашкой"
current:
<команда XY-pic> , <команда XY-pic> , ... <команда XY-pic> { , }
<команда XY-pic> ; <команда XY-pic> ; ... <команда XY-pic> { ; }
{ <команда XY-pic> } , { <команда XY-pic> } , ... { <команда XY-pic> } { , }
Здесь используются команды
, и
;, которые каждый раз позволяют "черепашке" двигаться заново из начала координат. Их отличие в том, что
, меняет только текущее положение черепашки
current, а
; каждый раз ещё сохраняет предыдущее положение в
previous (точнее, обменивает значения
current и
previous). Фигурные скобки
{ } позволяют группировать команды, так что группа не влияет на предыдущее значение
previous. Полный допустимый синтаксис см. в [RM].
<
Команда XY-pic> в простейшем случае имеет вид:
{ <задания координат> ... } { <рисование объектов> ... }
"Черепашка"
current устанавливается в заданное положение, и в нём рисуется объект. Несколько <
заданий координат> позволяет откладывать нужную точку от какой-то ещё. В одном положении можно нарисовать несколько объектов.
3.1. Как перемещаться по рисунку<
Задание координат> (в [RM] - <
coord>, fig. 1 p. 8) имеет разные формы, например:
( <координата по x> , <координата по y> ) - задаёт точку по её координатам (в системе координат base)
a( <угол в градусах (целый)> ) - откладывает единичный вектор в заданном направлении (то есть эквивалентно (  ,
,  ))
))
"<имя точки>" - переходит в точку, которой ранее было присвоено имя (см. 3.6 и подпункт "важно")
p - переходит в точку previous
c - переходит в точку current, то есть остаётся на месте. Также вместо c можно ничего не писать.
Можно комбинировать эти формы, последовательно смещаясь на соответствующие векторы:
<задание координат> + <задание координат> ...
<задание координат> - <задание координат> ...
Можно изменить систему координат
base, поставив в цепочку <
заданий координат> такую конструкцию:
{ <положение начала координат> ; } <единичный вектор по x> : { <единичный вектор по y> :: }
Если не задать <
положение начала координат>, будет использовано текущее значение
previous. Если не задать <
единичный вектор по y>, он будет отложен от <
единичного вектора по x> перпендикулярно против часовой стрелки.
3.2. Как создавать объектыПо каким-то причинам, синтаксически объекты в XY-pic бывают двух типов, в [RM] обозначенных как <
object> и <
decor>
ation. <
Object> - более простые и базовые, <
decor> - сложные и составные. <
Object> ([RM] 4 p. 11 и fig. 3 p. 12) можно нарисовать так: установив "черепашку"
current в нужное положение, в этом положении можно "сбросить" объект командой вида
Конкретные объекты бывают такие:
* { <произвольная формула LaTeX> }
* <библиотечный объект>
В качестве формул удобны одиночные значки, которыми можно отмечать точки:
*{\bullet},
*{+},
*{\times},
*{\circ},
*{\square} и т. п. См. руководство по формулам. Также можно использовать прямо буквы и цифры. С помощью этого же типа объектов можно рисовать подписи к точкам и другим объектам, как будет показано в 3.4.
Библиотечные объекты здесь - кружки и рамки, они описаны в 4.1 и имеют базовый вид
*\cir{},
*\frm{ <
мнемоника рамки>
}. Их удобно применять, чтобы рисовать буквы в кружках, и т. п. Их особенность состоит в том, что они комбинируются с другими, ранее нарисованными объектами.
<
Decor> можно нарисовать так: установив "черепашку"
current в нужное положение, написать команду объекта - что-то вроде
{ <
команда объекта> <
дополнительные данные> ...
}. Если объект изображается в самом конце рисунка XY-pic, или после него идут только другие такие объекты (но не перемещения "черепашки"
current), то фигурные скобки не обязательны. Конкретные объекты бывают разнообразные:
\ar,
\xypolygon,
\xymatrix,
\ellipse - они описаны в разделе 4. Есть и другие объекты, более экзотические, с ними можно познакомиться в [RM], хотя многие из них на форуме недоступны.
Некоторые объекты можно "рисовать" невидимыми, так чтобы они только задавали расположение на холсте некоторых точек, и потом ссылаться на эти точки для дальнейшего рисования.
Замечание для чтения [RM]: <Decor> можно написать без фигурных скобок, но тогда этой командой последовательность <команд XY-pic> будет закончена. Можно будет только поставить несколько <decor> подряд. Чтобы этого не случилось, <decor> и следует брать в фигурные скобки { }, поскольку тогда последовательность <команд XY-pic> заканчивается только внутри фигурных скобок, но не снаружи. Также, существует возможность возобновить последовательность <команд XY-pic> после "переключения в режим <decor>": специальная <decor>-команда \POS. Эти возможности часто используются в примерах в [RM], но здесь я описываю простейший способ использовать XY-pic.
Пример 1: Перемещение по рисунку и "сброс" объектов.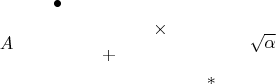
$$\begin{xy} /r1cm/:,
(0,0.75)*{A}, % рисование буквы A в математическом стиле
(1,1.5)*{\bullet}, % рисование жирной точки, и т. д.
(2,0.5)*{+}, (3,1)*{\times}, (4,0)*{*},
(5,0.75)*{\sqrt{\alpha}}, % можно рисовать и более сложные формулы
\end{xy}$$
Здесь вы видите последовательность команд вида
<задание координат> <рисование объекта> , ...
где объект рисуется как
Скучновато, но что поделаешь. Дальше будет больше возможностей.
3.3. Как размещать объектыОбъект <
object>, с точки зрения XY-pic, имеет форму и размеры, которые по умолчанию соответствуют тому, как объект выглядит, но могут быть скорректированы. Где-то внутри формы объекта находится его точка привязки, по умолчанию в центре. Когда объект "сбрасывается", он устанавливается своей точкой привязки в положение
current. Но это можно изменить, как и сдвинуть положение
current как-то по отношению к границам объекта, для дальнейшего использования. (Полный синтаксис - [RM] fig.3 p. 12, <
modifier>.)
Чтобы сместить объект перед "сбросом", используется конструкция
* { ! <буква угла> { ( <множитель> ) } } <объект>
<
Буква угла> бывает
L,
R,
U,
D, их двухбуквенные сочетания или
C. После смещения, точка привязки объекта оказывается в соответствующем углу (или смещается пропорционально заданному <
множителю>):
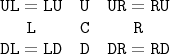
Можно изменить размеры объекта, как их воспринимает XY-pic, перед тем, как смещать его (также это повлияет на линии, которые проводятся до границы объекта). Это делается так:
* { <изменения размера> ... } ! <буква угла> <объект>
где <
изменение размера>:
+ { < <величина длины для LaTeX> > } - раздвинуть границы, по умолчанию на 3pt
- { < <величина длины для LaTeX> > } - сжать границы, умолчание такое же
= { < <величина длины для LaTeX> > } - установить заданный размер
= 0 - установить нулевой размер
Заметьте, изменений размера может быть несколько. Вот как выглядят увеличения на один плюсик, два плюсика, три плюсика:
 3.4. Как создавать текстовые метки
3.4. Как создавать текстовые меткиВсё необходимое уже есть в 3, 3.2 и 3.3, так что осталось только собрать всё вместе (привожу здесь, чтобы пользоваться как шаблоном):
{ <задания координат> ... } { * { <формула LaTeX для точки> } } * { <изменения размера метки> ... } ! <буква угла метки> { <формула LaTeX для метки> } ...
Пример 2: Объекты и текстовые метки.
$$\begin{xy} /r1cm/:,
(1,1.5) *{\bullet} *+!UR{A}, % сначала ставится точка, а потом, со смещением - надпись A
(2,0.5)*{+}*++!D{B}, (3,1)*{\times}*+!UL{q_{k\ne m}}, (4,0)*{*}*++!L{\gets\text{ безумие какое-то}}, (5,1)*{\bullet}*++!D{\downarrow}*++++++!D{\text{еще одно}},
\end{xy}$$
Здесь вы видите отступы, подобранные так, чтобы они красиво выглядели. И в конце - пример, когда к точке добавляются две метки.
3.5. Как создавать линииЗдесь описано рисование простых прямых линий и стрелок из одной точки в другую. Изогнутые и другие сложные стрелки см. в 4.2, разнообразные кривые линии - в 4.5 и 4.6.Для рисования линий потребуются две новые концепции: рисование соединения между двумя точками,
current и
previous, и рисование специального вида объектов, <
направленного объекта>, который поворачивается в зависимости от заданного направления (по умолчанию подразумевается направление вектора из
previous в
current). Эти концепции вместе дают возможность рисовать линии. <
Направленные объекты> сами по себе дают возможность рисовать стрелочки на кончиках линий.
Соединение между точками
current и
previous использует специальную форму "сброса" объекта
При этом рисуется не один объект в точке
current, а много объектов вдоль прямой линии между
current и
previous:
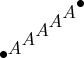
<
Направленный объект> (в [RM] - <
dir>, 6.1 p. 16 и fig. 5 p. 17) - это ещё один библиотечный объект, кроме упомянутых в 3.2. Он меняет свой вид в зависимости от текущего направления, так что позволяет рисовать сегменты линий и стрелочки на концах линий. Текущее направление при этом выставляется по вектору из
previous в
current. Этот библиотечный объект можно создавать по полному имени
\dir или по сокращённому синониму
@ (это одно и то же, очень неразборчиво сформулировано в [RM] fig. 3 p. 12, строка 4). Дальше я буду упоминать только сокращённую форму
@. Формат:
@<вариант направленного объекта>{<мнемоника направленного объекта>}
Итак,
для рисования линии (предварительно установив
previous и
current) надо написать:
** @<вариант направленного объекта>{<мнемоника направленного объекта>}
Если
previous и
current не установлены, можно их установить командой
; (с отсутствующей командой рисования в первой точке), так что получится:
<задание координат previous> ; <задание координат current> ** @<вариант направленного объекта>{<мнемоника направленного объекта>}
Для
рисования кончика стрелочки в положении
current надо написать:
* @<вариант направленного объекта>{<мнемоника направленного объекта>}
Для
рисования начала стрелочки см. 3.7, 3.8, или можно использовать шаблон:
?(0) * __ @<вариант направленного объекта>{<мнемоника направленного объекта>}
<
Вариант направленного объекта> может быть пустым, или одним из символов
^,
_,
2,
3. Соответственно, рисуются обычная линия / стрелочка, верхняя половинка, нижняя половинка, двойная или тройная линия.
<
Мнемоника направленного объекта> указывает, что именно будет нарисовано. <
Мнемоники направленного объекта> для рисования линий и стрелочек разные, хотя
{} всегда рисует пустой объект. Для линий:
{.},
{-},
{~},
{--},
{~~} - дают линию из точек, сплошную, волнистую, и штриховые варианты сплошной и волнистой (для удобства определены ещё
{:},
{=},
{==}, дающие двойные варианты
{.},
{-},
{--}). Для стрелочек:
{>},
{<},
{|},
{+},
{x} - рисуют то, что ожидается,
{*} и
{o} - сплошной и пустой кружочек. Более полные списки см. 6.1.
Пример 3: Линии.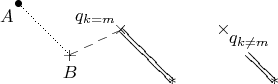
$$\begin{xy} /r1cm/:,
(1,1.5) *{\bullet} *+!UR{A}; % размещаем точку и надпись, как в примере 2
(2,0.5) **@{.} *{+} *++!U{B}; % переходим в новую точку, проводим линию от прежней, и рисуем остальное
(3,1) **@{--} *{\times} *+!DR{q_{k=m}}; (4,0) **@{=} *{*};
(5,1) *{\times} *+!UL{q_{k\ne m}}; (6,0) **@{=} *{*}; % эта строчка почти повторяет предыдущую
\end{xy}$$
Наконец-то мы можем рисовать почти всё, что захотим. Было бы терпение. Обратите внимание, что линия не проходит по области, занятой размерами тех объектов, которые были нарисованы в положениях
previous и
current (только того объекта в
current, который уже нарисован, а не того, который будет нарисован позже). Это видно на иллюстрации:
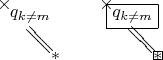
Если это мешает, можно установить размер объекта в нуль:
* { <изменения размера> ... } ! <буква угла> =0 <объект>
Тогда получится:
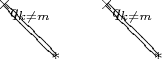
Также можно изменить порядок рисования. Других объектов, кроме
previous и
current, линия не знает и не учитывает, может их перекрывать (бороться с этим можно порядком рисования и использованием рамок, см. 4.1).
Пример 4: Плоский график.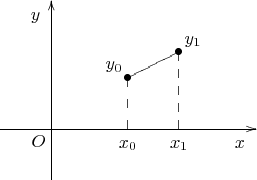
$$\begin{xy} /r1cm/:,
(0,0)*+!UR{O}, % обозначение начала координат
(-1,0);(4,0)**@{-}*@{>}*++!UR{x}, % ось x с надписью
(0,-1);(0,2.5)**@{-}*@{>}*++!RU{y}, % ось y с надписью
(1.5,0)*++!U{x_0}; % встаём в начальную точку на оси x
(1.5,1)*{\bullet}*+!DR{y_0}**@{--}; % вертикальная линия вверх
(2.5,1.5)*{\bullet}*+!DL{y_1}**@{-}; % наклонная линия
(2.5,0)*++!U{x_1}**@{--}; % вертикальная линия вниз до оси x
\end{xy}$$
![$$\begin{xy} /r1cm/:,
(0,0);p+(2,-1)**@{-};p+(3.5,1.5)**@{-};p-(2,-1)**@{-};p-(3.5,1.5)**@{-}; % рисование плоскости
(1.5,0.25);p+(1,-0.5)**@{-}*@{>}*+!L{\mathbf{a}}; % рисование вектора a
(1.5,0.25);p+(2,0)**@{-}*@{>}*+!L{\mathbf{b}}; % рисование вектора b
(1.5,0.25);p+(0,2)**@{-}*@{>}*+!DR{[\mathbf{ab}]}; % рисование вектора [ab]
\end{xy}$$ $$\begin{xy} /r1cm/:,
(0,0);p+(2,-1)**@{-};p+(3.5,1.5)**@{-};p-(2,-1)**@{-};p-(3.5,1.5)**@{-}; % рисование плоскости
(1.5,0.25);p+(1,-0.5)**@{-}*@{>}*+!L{\mathbf{a}}; % рисование вектора a
(1.5,0.25);p+(2,0)**@{-}*@{>}*+!L{\mathbf{b}}; % рисование вектора b
(1.5,0.25);p+(0,2)**@{-}*@{>}*+!DR{[\mathbf{ab}]}; % рисование вектора [ab]
\end{xy}$$](https://dxdy-03.korotkov.co.uk/f/2/2/c/22cfc6c1024b0c6154b3d8d410aad62c82.png)
$$\begin{xy} /r1cm/:,
(0,0);p+(2,-1)**@{-};p+(3.5,1.5)**@{-};p-(2,-1)**@{-};p-(3.5,1.5)**@{-}; % рисование плоскости
(1.5,0.25);p+(1,-0.5)**@{-}*@{>}*+!L{\mathbf{a}}; % рисование вектора a
(1.5,0.25);p+(2,0)**@{-}*@{>}*+!L{\mathbf{b}}; % рисование вектора b
(1.5,0.25);p+(0,2)**@{-}*@{>}*+!DR{[\mathbf{ab}]}; % рисование вектора [ab]
\end{xy}$$
Здесь конструкции вида:
в сочетании с командой
; используются для перехода от точки к точке на относительные смещения. См. 3.1.
(Переместить раздел в другое место)
Маленькие хитрости:Чтобы нарисовать значок перпендикулярности на планиметрическом чертеже... (Не написано.)
На стереометрическом чертеже... (Не написано.)
Дужки углов на планиметрическом чертеже... (Не написано.)
Дужки углов на стереометрическом чертеже... (Не написано.)
3.6. Как именовать положенияВажно! Если в рисунке XY-pic используются имена, то стандартное обрамление рисунка XY-pic на форуме меняется следующим образом:[math]$$\shorthandoff{"}\begin{xy} /r1cm/:, <команды XY-pic> ... \end{xy}\shorthandon{"}$$[/math]
где команда /r1cm/:, может быть модифицирована, как описано в 1. Также, в режиме предпросмотра после картинки будет выдан лишний мусор, хотя сама картинка будет отображена нормально. Не нужно его пугаться. При окончательной отправке сообщения на форум он исчезнет. И наконец, тег alt для такой картинки не будет сформирован правильно.Любую точку можно обозначить именем, и позже возвращаться в него, используя это имя. Для задания нового имени в <
команде XY-pic>, как она описана в 3, добавляется такая конструкция:
{ <задания координат> ... } = "<имя точки>" { <рисование объектов> ... }
{ <задания координат> ... } { <рисование объектов> ... } = "<имя точки>"
При этом имя присваивается тому положению
current, которое было установлено в момент задания имени. Если имя присваивается после рисования объекта, оно запомнит также форму и размеры этого объекта. Имена можно переопределять, тогда будет использоваться последнее определённое значение. Чтобы перейти в точку с именем, используется форма <
задания координат>, уже упоминавшаяся в 3.1:
"<имя точки>" - переходит в точку, которой ранее было присвоено имя
Переход в точку, имя которой ранее не было определено - ошибка.
3.7. Как перемещаться по рисунку - продвинутые способы(Не написано.)
[RM] 3n p. 10: Формы <
задания координат> вида
+ <
буква угла> {
( <
множитель>
) } и
! <
буква угла> {
( <
множитель>
) }
[RM] 3h p. 9: Формы <
задания координат> вида
?( <
фактор alpha>
),
? < ...,
? > ..., и
? ...
/ <
расстояние LaTeX>
/Необходимость соединения для
? ..., пустое соединение
**{}Формы <
задания координат> вида
? ... для кривых - ссылка на 4.6
[RM] 3j p. 9: Форма <
задания координат> вида
?!{ <
начало>
; <
конец>
} для поиска точки пересечения двух прямых
3.8. Как модифицировать объекты - продвинутые способы(Не написано.)
[RM] 4j p. 13: Изменение формы объекта
* [ <
мнемоника формы>
] <
объект>
[RM] 4f p. 13: Изменение точки привязки объекта
* ! <
буква угла> {
( <
множитель>
) } <
объект> и
* ! <
произвольный вектор> <
объект>. Отличие от
* <
объект>
! <
буква угла> {
( <
множитель>
) }, описанной в 3.7.
[RM] 4l 4m p. 14: Изменение направления для объекта: установка <
буквой направления>,
va( <
углом в градусах>
), модификация
^,
_,
:a( <
углом в градусах>
). Зачем это нужно: использование в стрелках 4.2 [RM] 24p p. 43
Продолжение
post544572.html#p544572