1. Prove that in an electrical network consisting of resistors only, the distribution of currents is such that the heat generated by them is minimal with constant total current.
2. In an electrical network, two arbitrary nodes are chosen and a resistor is added. Prove that the total resistance wasn't raised.
1. For generality(and also for simplicity) instead of scheme of resistors consider a conducting media with electrical resistivity
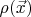
. The produced heat is given by the following integral:
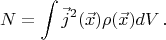
And the condition of constancy of the total current reads
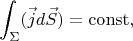
where the integration goes over an arbitrary intersection

of the domain. The extremum of

is achieved for distributions
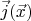
such that

for arbitrary variation
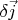
, which satisfies

and also boundary conditions for
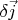
.
Let us write down the condition (1). For given a variation let us consider a narrow current tube along
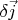
(
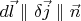
, see pic.).

One can write the following transformation

From (2) it follows that
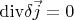
. Taking in account that
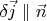
we conclude that along any intersection of the tube we have
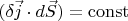
.
Thus, in (3) we can first integrate by

:
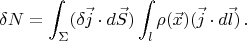
:
Taking in account (2) we conclude that the condition
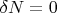
is satisfied if we require
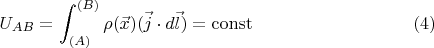
along any current line
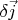
. Since
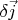
is arbitrary, the euqality (4) should be satisfied for any circuit with fixed ends and defines the electrical potential difference between the points

and

. Thus, the extremum of the produced heat in an electrical network is achieved only in case of satisfying the Kirchhoff's circuit laws: conservation of current(
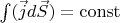
) and the potentiality of the field-
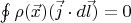
for any closed circuit.
-- Вс янв 22, 2012 18:54:26 --Я тут пересказывл своему приятелю, вот и решил перевести.
