первое начало термодинамики

[AndreyL]

Друзья, всех с наступившим Новым Годом!

Вопрос по термодинамике. Во всех учебниках рассматриваются процессы либо изотермические, либо изобарические, либо изохорные, либо адиабатические. А как быть, если все меняется? Например так: есть резервуар с поршнем, поршень сжимает пружину, т.е. давление на поршень может быть описано линейной зависимостью от давления. Резервуар заполнен газом, в него вставлен нагреватель. Потерь тепла через стенки резервуара нет, химических превращений нет (это можно будет потом ввести). Как записать уравнения, связывающие внутреннюю энергию, давление, температуру, объем газа и теплоту, переданную нагревателем? Газ для простоты идеальный, потом заменим Ван-дер-Ваальсовским.

[Himfizik]

В чем вопрос? Как записать $I$ начало термодинамики?
$\delta Q= dU+dA$ - в дифференциальной форме, $\Delta Q=\Delta U+A$ - в интегральной форме к определенному моменту времени, где $A=kx^2/2$.

[AndreyL]

Вопрос, скорее, в том, как расписать $dU$ через $dT$, $dp$ и $dV$ и подставить его в уравнение $\delta Q= dU+dA$. При этом частные производные $\frac{\partial U}{\partial T}$, $\frac{\partial U}{\partial p}$ и $\frac{\partial U}{\partial V}$ записать в виде чего-то осмысленного, поддающегося измерению. Например: $\frac{\partial U}{\partial T}$ есть теплоемкость, вот только какую теплоемкость тут использовать, теплоемкость при постоянном давлении, или при постоянном объеме?

[Himfizik]

AndreyL в сообщении #522473 писал(а):

Газ для простоты идеальный

Если так, то $dU=C_V dT$

AndreyL в сообщении #522473 писал(а):

потом заменим Ван-дер-Ваальсовским

А в этом случае придется использовать более общий подход термодинамических потенциалов. Знания уравнения состояния и $C_V$ как функции от $T$, достаточно для нахождения вида свободной энергии, энтропии, а значит и внутренней энергии. Задайте какой-нибудь "физический" вариант температурной зависимости $C_V$ (потом попробуйте добавить в этот закон давление), проведите расчет, посмотрите.
Правда там, если я не ошибаюсь, должна вылезти парочка констант интегрирования для свободной энергии и по одной константе для энтропии и внутренней энергии.

[AndreyL]

Хорошо, давайте для начала разберемся с идеальным.

Himfizik в сообщении #522521 писал(а):

Если так, то $dU=C_V dT$

Для изохорного процесса это совершенно справедливо, но тогда $dA=0$, что не соответствует нашему процессу. Или я не прав?

[Himfizik]

AndreyL в сообщении #522583 писал(а):

давайте для начала разберемся с идеальным

Давайте.

1 способ) По теореме о равнораспределении средней кинетической энергии по степеням свободы (см. курс статфизики), имеем, что на каждую степень свободы приходится по $kT/2$. В случае идеального газа, пренебрегая потенциальной энергией взаимодействия, считаем, что внутренняя энергия равна средней кинетической. Итак, $U=ikT/2$, где $i=i_\text{пост}+i_\text{вращ}+2i_\text{колеб}$ - суммарное число степеней свободы. Итого на один моль газа $U=iRT/2$, где $iR/2$ обозначают $C_V$.

2 способ) Выбираем переменные $T$ и $V$. Несложно получить равенство: $(\frac {\partial U}{\partial V})_T=T(\frac {\partial p}{\partial T})_V-p$, используя либо метод циклов Карно, либо технику якобианов, либо, что почти тоже самое, выражение для свободной энергии в естественных переменных. С учетом уравнения состояния идеального газа, получаем независимость $U$ от $V$.

[AndreyL]

Честно говоря, меня немного раздражают эти нижние индексы, насколько я понимаю, они нужны только для того, чтобы показать, какие переменные мы приняли как независимые. Т.е., например, в Вашем примере $(\frac {\partial U}{\partial V})_T$ нижний индекс $T$ означает только то, что давление у нас является функцией температуры и объема. Если не прав - поправьте, пожалуйста.
Теперь по существу. Попробуем решить при переменных $T$ и $p$ - пока мне так проще, далее попробую получить то-же самое при переменных $T$ и $V$. Имеем:

$$dU=\frac {\partial U}{\partial T}dT+\frac {\partial U}{\partial p}dp$$

$$\delta Q=dU+p dV$$

тогда:

$$\delta Q=\left(\frac {\partial U}{\partial T}+p\frac {\partial V}{\partial T} \right) d T + \left(\frac {\partial U}{\partial p}+p\frac {\partial V}{\partial p} \right) d p$$

с учетом уравнения состояния идеального газа и $\frac {\partial U}{\partial T}=C_V$(не знаю, правильно ли это, в свое время мне эти "при постоянном давлении" и "при постоянном объеме" все мозги узлом завязали), а также независимости внутренней энергии идеального газа от объема и давления $\frac {\partial U}{\partial p}=0$

$$\delta Q=\left(C_V+R \right) d T - \frac {\R T}{p} d p$$

А вот что с этим делать дальше - не очень понятно. По идее у меня не задействовано уравнение для пружины, и задействовать его надо было где то в самом начале.

[AndreyL]

Если я правильно понимаю, то независимая переменная должна остаться одна, поскольку на три переменные (температура, давление, объем) существует два уравнения: с одной стороны уравнение состояния, с другой уравнение давления пружины. Выбрав при решении любую из переменных в качестве независимой мы должны получить один и тот же ответ для всех трех. Или я ошибаюсь?

[Munin]

AndreyL в сообщении #522730 писал(а):

Честно говоря, меня немного раздражают эти нижние индексы, насколько я понимаю, они нужны только для того, чтобы показать, какие переменные мы приняли как независимые.

Тем не менее, они нужны, поскольку одного обозначения частной производной не хватает, чтобы указать весь список независимых переменных.

[AndreyL]

Munin в сообщении #522775 писал(а):

Тем не менее, они нужны, поскольку одного обозначения частной производной не хватает, чтобы указать весь список независимых переменных.

Да, но при расчете в матпакетах нижние индексы никуда не вставишь, я так понимаю, что они нужны только на бумаге.
Однако сейчас больше интересует вопрос - как решить конкретную задачу.

[Munin]

(Оффтоп)

AndreyL в сообщении #522808 писал(а):

Да, но при расчете в матпакетах нижние индексы никуда не вставишь

Там приходится более неудобными способами выкручиваться, вы правы.

[Himfizik]

AndreyL в сообщении #522730 писал(а):

А вот что с этим делать дальше - не очень понятно. По идее у меня не задействовано уравнение для пружины, и задействовать его надо было где то в самом начале.

Я снова перестаю понимать цель Вашей задачи. Если Вы хотите получить выражение в частных производных, приводящее Вас к независимости $U$ от $p$, то это еще мне понятно и это согласуется с Вашим

Himfizik в сообщении #522480 писал(а):

Вопрос, скорее, в том, как расписать $dU$ через $dT, dp$, и $dV$

Что вы пытаетесь с пружиной сделать в этой постановке я уже не понимаю. По мне так, приговариваете при решении задачи, мол, процесс можно рассматривать как отдаленно похожий на квазистатический. В произвольный момент времени записали условие "квазиравновесия" $kx=ps$, отсюда $pdV=kxdV/s=kxdx$ и при интегрировании $A=kx^2/2$. Это отдельная часть задачи, называется вычисление работы газа. Если я не прав, пусть меня поправят.

Теперь Вы взялись за вид $U$ от механических и тепловых переменных в случае идеального газа. Этот вид можно определить имея в распоряжении уравнение состояния. Кроме того, Вам нужно выбрать тот аппарат получения соотношения (из второго способа), который Вам знаком. С якобианами у Вас как? С термодинамическими потенциалами? Кстати, вы случайно не химик, у них вроде как такая сильная любовь к переменным $T$ и $p$ (на решение задачи это отразится только в рассмотрении, например, не свободной энергии, а потенциала Гиббса)?

[AndreyL]

Прошу прощения, если я не очень понятно объясняю - по образованию я не физик и не химик. Моя задача чисто теоретическая - при чтении учебников возникла мысль, что изобарно-изотермическая задача (с потенциалом Гиббса), изохорно-изотермическая (с потенциалом Гельмгольца) и вообще все изо-задачи есть частные постановки одной общей задачи. Вот и хочу попробовать решить задачу не при постоянных давлении или объеме, а при связанных, тогда все изо-задачи будут просто ее частным случаем. Начал с самого простого варианта, потом попробую усложнить.
С якобианами у Вас как?
Тут как раз все просто - современные матпакеты способны брать производные и от векторных функций
Кстати, вы случайно не химик, у них вроде как такая сильная любовь к переменным $T$ и $p$ (на решение задачи это отразится только в рассмотрении, например, не свободной энергии, а потенциала Гиббса)?
Никакой любви нет, наоборот, как раз хотелось бы избежать частных постановок.

Далее до чего пока дошел. Если возможно, подскажите, пожалуйста, насколько правомочно такое решение.
В общем виде имеем:

$$dU=\frac {\partial U}{\partial T}dT+\frac {\partial U}{\partial p}dp+\frac {\partial U}{\partial V}dV$$

$$\delta Q=dU+p dV$$

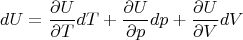
есть большое подозрение, что для идеального газа последние два слагаемых равны нулю, но пока оставим

Еще уравнение состояния идеального газа и уравнение, связывающее давление с объемом в виде $p=p_0+k(V-V_0)$ - для простоты назовем их связывающими уравнениями (не знаю, как правильно назвать). В качестве независимой переменной выбираем, к примеру, давление. Из связывающих уравнений находим $T=\frac{p (k V_0+p-p_0)}{k R}$ и $V=\frac{k V_0+p-p_0}{k}$. Подставляем это в уравнение для дифференциала внутренней энергии. Частные производные остаются на месте, меняются только полные дифференциалы, а именно $dT=\frac{k V_0+2 p-p_0}{k R} dp$ и $dV=\frac{dp}{k}$. Точно так же меняется полный дифференциал объема в уравнении для $\delta Q$. Далее подставляем внутреннюю энергию в уравнение теплоты, и с учетом $\frac {\partial U}{\partial T}=C_V$, $\frac {\partial U}{\partial p}=0$ и $\frac {\partial U}{\partial V}=0$ имеем:

$$\delta Q=\frac{C_V (k V_0+2 p-p_0)+p R}{k R}dp$$

Интегрируя $\Delta Q=\int_{p_0}^{p_1} \frac{C_V (k V_0+2 p-p_0)+p R}{k R} \, dp$ находим $p_1$, и, используя связывающие уравнения $T_1$ и $V_1$.

[Himfizik]

Как то мне Ваше уравнение, связывающее давление и объем, не нравится. Какими соображениями Вы пользовались? Оно, мне так кажется, или с идеальностью газа как-то не очень "дружит" или и с реальным миром.

[AndreyL]

Himfizik в сообщении #523099 писал(а):

Как то мне Ваше уравнение, связывающее давление и объем, не нравится. Какими соображениями Вы пользовались? Оно, мне так кажется, или с идеальностью газа как-то не очень "дружит" или и с реальным миром.

Согласен с Вами полностью, тоже пока ничего понять не могу. Просчитал эту схему при независимых температуре, давлении и объеме поочередно. Расчеты при независимых давлении и объеме между собой сходятся, а вот при температуре сходится к предыдущими только в случае $k=\frac {p_0}{V_0}$.
Соображения следующие. В нулевом состоянии существует некоторое давление внешней среды, но поршень только касается пружины. При увеличении объема на поршень действует то-же самое давление внешней среды плюс давление пружины. Где-то ошибся, где - не соображу. Подскажите?