Вот не вижу причин, которые бы заставляли тащить Куна-Такера в плоскую задачу. Да даже и в более общем случае для начинающих полезнее разобраться с методом Лагранжа в оригинальной версии.
Требуется найти

и

функции непрерывной функции на компакте.
(Оффтоп)
И то и другое достигается в некоторой точке. Если эта точка внутренняя, то срабатывает необходимое условия равенства
нулю тех частных производных, которые существуют. А если она на границе, то это точка условного экстремума. В такой точке (явно или чисто теоретически по теореме о неявной функции)
можно часть переменных выразить через остальные. Точки нарушения условий существования неявной функции включаем в число проверяемых. Если явное выражение не получается
или неудобно или на то есть запрет от постановщика задачи, составляем функцию Лагранжа и ищем её критические точки. Граница может быть задана кусочно и в случае неплоской
задачи может возникнуть необходимость рассмотрения совместного выполнения нескольких уравнений связи. Вот только здесь и могут сказаться некоторые вычислительные преимущества
Куна-Такера перед Лагранжем.
В нашем случае целевая функция

, а ограничения даются неравенствами

Эти ограничения задают
"серпик", который впрочем рисовать не обязательно - так как всё лежит в круге, то область ограничена и замкнута, так как неравенства у нас нестрогие.
Тупо приравниваем к нулю частные производные целевой функции и получаем точку

, которая лежит вне области, следовательно искомая точка (минимума или максимума) лежит на границе.
(Оффтоп)
Если не тупо, то ещё очевиднее - во внутренней точке можно сдвинуться по вертикали вниз/вверх и получить большее/меньшее значение
Граница состоит из трёх кусков - кругового, параболического и прямолинейного. Для примера рассмотрим случай когда искомая точка лежит на окружности.
(Оффтоп)
Я бы просто заменил в целевой функции

на

и рассмотрел функцию одной переменной на понятно каком отрезке, но нам это запретили.
Функция Лагранжа для этого случая

. Приравниваем частные производные к нулю:

Если
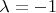
, то

- обе точки лежат ниже серпика. Если

, то

. Эта точка очевидного минимума. Остались ещё граничные точки дуги - это
точки пересечения окружности с параболой и прямой

и
