Добрый вечер.
Помогите, пожалуйста, решить вторую половину следующей задачи:
Ползун

, перемещаясь по прямолинейно направляющей, приводит в движение через стержень

колесо 1 радиуса

, которое катится без скольжения по неподвижному колесу 2 того же радиуса. В положении, указанном на рисунке, определить скорости и ускорения точек

и

, если в данный момент ползун

имеет скорость

и ускорение

. Длина стержня AB равна

м.
Изображение задачи:

Мое построенное изображение:

Констуркцию условно можно разбить на три части, обозначим их цифрами:
2 — стержень

, 1 — колесо с центром в точке

, 0 — стержень

.
Таким образом, для каждой

-той (

) части обозначим угловую скорость и угловое ускорение соответственно так:

и
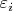
.
Обозначения:
W_A

и V_A

— ускорение и скорость точки A,
W_ц^A

и W_вр^A

— центростремительное и вращательное ускорения точки

относительно точки

,
W_ц1^P

и W_вр1^P

— центростремительное и вращательное ускорения точки

относительно точки

,
W_ц2^P

и W_вр2^P

— центростремительное и вращательное ускорения точки

относительно точки

,
W_ц1^B

и W_вр1^B

— центростремительное и вращательное ускорения точки

относительно точки

,
W_ц2^B

и W_вр2^B

— центростремительное и вращательное ускорения точки

относительно точки

,
точка P — мгновенный центр скоростей стержня AB, построенный как пересечение перпендикуляров к векторам скоростей точек A и B.

, следовательно, K — мгновенный центр скоростей.
На рисунке оранжевые элементы — это углы. Жирная дуга обозначает угол в 30 градусов, тонкая дуга — в 60 градусов, а полуквадрат — прямой угол.
Дополнительно найденные длины:

,

,

.
Скорости точек C и B я нашел по формуле Эйлера (

,

), заодно найдя угловые ускорения каждой части конструкции:


(через проекцию на ось x, отмеченную на рисунке).

(вот тут еще
вопрос: если рассматривать

, то получается, что

, как это объяснить?)
Чтобы найти ускорения точек, надо знать угловые ускорения конструкций 1 и 2. Если известно одно из них, то найти можно и второе.
Но как найти угловое ускорение? Явно надо использовать данное ускорение точки A, но не знаю, как.
Пробовал рассматривать точку P:

и

Проецируя на оси, получаем систему двух уравнений относительно двух угловых ускорений

и

, но она либо не имеет решения (уравнения образуют параллельные прямые), либо бесконечное число решений (совпадают прямые)...
Думалось, что, может, как-то надо отталкиваться от точки K, но я не знаю, куда у нее направлено ускорение. Если логически, то ведь

(разложение на нормальное и тангенциальное ускорения), где

, тогда ускорение состоит только из тангенциальной (
правильно ли это?), направленной по касательной у закрепленной окружности, но я без понятия, как ее найти, чтобы найти угловые ускорения из равенства:

проекцируя их, получается система с тремя неизвестными (угловые ускорения и тангенциальное ускорение точки K), ничего из нее не найти...
Использовать разложение на нормальное и тангенциальное ускорения для других точек не знаю, т.к. трудно представить, по какой траектории они движутся (кроме точки A).
Как быть?
P.S. Ответ должен получиться

и
