Доказательство, множества

[Unconnected]

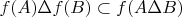
Доказать, что $f(A)\Delta f(B) \subset f(A\Delta B)$. Как бы понятно, что слева элементов может быть меньше, чем справа, т.к. элементы из пересечения игриков могут быть получены из не-пересекающихся иксов тоже. Доказать пробую так:
$f(A)\bigcap f(B)\neq \oslash \Leftrightarrow A\bigcap B\neq\oslash \Rightarrow f(A)\Delta f(B)=\left \{ f(x)|x\notin A\bigcap B\right \}$ - а множество справа состоит из таких же считай иксов. Это похоже на правду?

[Хорхе]

Не похоже. Уже первый значок эквивалентности неправильный, более того, к задаче он не имеет никакого отношения.

[Unconnected]

Да, он как раз противоречит возможности не-биективности.. можно указание какое-нибудь?

[Unconnected]

Вроде доказал, рассмотрев два случая: когда прообраз игрика из пересечения лежит только в пересечении иксов, и когда ещё где-нибудь лежит.