Удивительное в теории вероятностей

[radiusR]

Здравствуйте! Помогите пожалуйста решить такую проблему с пониманием непрерывных случайных величин в теории вероятностей, хотя это можно назвать и задачей.
Все мы знаем, что функция распределения задается как $F_\xi (x) = P\left\{\xi < x\right\}$. А также известно, что для непрерывных распределений $P\left\{\xi = x\right\} = 0$ при любых значениях $x$. Но если подставить в данную функцию $\xi$, то получим: $f(\xi)=P\left\{\xi = \xi\right\} = 1$ . То есть тождественно равная нулю функция вдруг стала равной 1. Думается мне, что дело в том, что такое подставление некорректно, а вот почему оно некорректно, для меня большая загадка, в каком направлении двигаться? Заранее спасибо.

[ewert]

radiusR в сообщении #505600 писал(а):

$P\left\{\xi = x\right\} = 0$ при любых значениях $x$. Но если подставить в данную функцию $\xi$,

А на каком основании подставлять? Что такое $\xi$ в той формуле -- и что такое $x$?...

(прочитайте, в чём состоит событие $\{\xi=x\}$ -- и в чём событие $\{\xi=\xi\}$; вслух прочитайте, с выражением)

[radiusR]

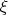
$\xi $ - это случайная величина с непрерывным распределением. $x$ - любое число из множества действительных чисел.
Событие $\left\{\xi = x \right\}$ означает, что случайная величина принимает значение $x$, а про $\left\{\xi = \xi \right\}$ я затрудняюсь точно сказать, возможно разве что случайная величина принимает значение, равное себе.
Я имел ввиду не какое-то конкретное задание, а проанализировать случайные величины. Мы просто задали функцию $f(x) = P\left\{\xi = x \right\}$ и, основываясь на том, что данная случайная величина непрерывна, положили, что эта функция тождественно равна 0. Но ежели вместо $x$ подставить случайную величину (точнее её значение), то получается то, что было описано выше. Или же здесь имеет место какая-то иллюзия: $\xi$, которую мы подставляем - это значение случайной величины в определенный момент времени, то есть просто действительное число, а $\xi$ слева - это сама случайная величина?

[Null]

$[f(\xi)](\omega)=P\left\{\xi = \xi(\omega)\right\} = 0$ - случайная величина всегда равная 0.

[Хорхе]

Да не забивайте голову всякой ерундой. Уравнение $x^3 = a$ имеет одно решение, уравнение $x^3=x$ -- три решения, а $x^3=x^3$ -- бесконечно много решений. Ничего необычного в этом нет.

[ewert]

radiusR в сообщении #505696 писал(а):

Но ежели вместо $x$ подставить случайную величину (точнее её значение),

Выберите что-то одно: или саму величину, или её значение. Это принципиально разные утверждения.

[radiusR]

ewert в сообщении #505706 писал(а):

Выберите что-то одно: или саму величину, или её значение.

Я предполагаю, что саму случайную величину мы просто не можем подставить, так как она является функцией, а $f(x)$ имеет аргументы из действительных чисел. Тогда если подставлять туда просто значение этой величины, тогда $f(\xi)$ в этом случае будет равняться нулю? То есть проблема с пониманием была связана именно с ошибкой интерпретирования разницы между случайной величиной и ее значением?

[--mS--]

radiusR в сообщении #505696 писал(а):

Или же здесь имеет место какая-то иллюзия: $\xi$, которую мы подставляем - это значение случайной величины в определенный момент времени, то есть просто действительное число, а $\xi$ слева - это сама случайная величина?

Конечно, иллюзия: $f(x)=\mathsf P\{\omega\in\Omega~ |~\xi(\omega)=x\}$. Для каждого $\omega_0\in\Omega$ берём вместо $x$ число $\xi(\omega_0)$ и получаем

$$f(\xi(\omega_0))=\mathsf P\{\omega\in\Omega~ |~\xi(\omega)=\xi(\omega_0)\}=0,$$

как и равнялась. Тщательнее, и не нужна будет никакая философия.

[Хорхе]

Теория вероятностей тут не при чем. У Вас проблемы с общей логикой.

Вернемся к моему примеру. Утверждение "уравнение $x^3=a$ имеет единственное решение" верно (если речь идет о действительных числах). Вот подставим в это утверждение $x$ или $x^3$ или даже $x^3+1$ вместо $a$ (почему нет, оно ведь любое) и получим ерунду.

Короче говоря, нельзя вот так произвольно подставлять что угодно куда угодно.

[radiusR]

Большое всем спасибо, очень помогли с пониманием данной темы!