Я сегодня утром, пока в универ ехал, разобрался с задачей.
Пусть

- искомое количество способов.
Тогда:

Почему так:
Как мы можем получить последовательность из

элементов. Во-первых, если у нас есть любая последовательность из

элементов, удовлетворяющая условие, то мы можем вставить в неё элемент в одну из

позиций ( так как всего позиций

, но одна позиция находится после элемента n-1, значит туда вставить n мы не можем). Это есть слагаемое

.
Во-вторых, для любой последовательности из

элементов, где ровно одна пара элементов нехорошая ( тоесть это последовательные два числа), мы можем вставить элемент n, разбив эту пару, и соответственно получим последовательность из

элементов удовлетворяющую условию. Теперь надо ответить на вопрос, сколько есть таких ( с одной нехорошей парой=) последовательностей из

элементов.
Для этого, зафиксируем любую пару последовательных элементов k, k+1 . Количество последовательностей с этой парой будет равно
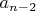
, и, так как пару k, k+1 из

элементов мы можем выбрать

способами, то вот мы и получили слагаемое

Таким образом:

.

Теперь, кто бы помог избавится от рекурентности в этой формуле?)