Для поля

надо составить матрицу размера

где номера строк/столбцов соответствуют клеткам на исходном поле. Элемент

в этой матрице равен 1, если нажатие на клетку номер

инвертирует клетку

, и 0 в противном случае.
Если эта матрица имеет полный ранг над полем
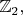
то достичь любой конфигурации клеток из любой исходной - можно, иначе - нет.
Вот еще одна аналогичная головоломка, кстати:
http://bz.var.ru/comp/web/js/floor.htmlДобавлено спустя 9 минут 25 секунд:В случае ладьи ответ на первый вопрос зависит от четности

Если

четно, то ответ "можно", если нечетно - "нельзя".
Подробно мы эту задачу когда-то разбирали
тут.
Добавлено спустя 3 минуты 23 секунды:Простейший алгоритм для ладьи в случае четного

такой (предполагая, что цвета - это числа 0 или 1, и что нам нужно привести поле к нулевому):
Hазовем клетку(ручку) "нечетной", если сумма всех чисел, стоящих с ней в одной строке или столбце нечетна. Алгоритм состоит в поворотах "нечетных" ручек. Hетрудно видеть, что при таком повороте ручка перестает быть "нечетной", а все остальные ручки сохраняют свою "четность". Поэтому с каждым поворотом число "нечетных" ручек уменьшается на 1 и в конце концов становится равным 0. Hу и последнее наблюдение: состояние без "нечетных" ручек только одно - нулевое.Этот алгоритм дает ответ на третий вопрос в случае ладьи и четного

: минимальное число ходов равно числу "нечетных" клеток.