Спасибо за предварительное обсуждение, по его итогам выношу на обсуждение улучшенный алгоритм и доказательство - не взыщите строго: какое было обсуждение, такие и итоги

Пусть графы

изоморфны. Для выбранной пары вершин

с равными степенями строим биграф

, где

- множество вершин графа

,

- множество вершин графа

, и вершина

соединена ребром с вершиной

, если у вершин

одинаковая степень и для элементов матриц

:

. Число ребер биграфа не будет превосходить

. Очевидно, что для единичных векторов

решения СЛУ

будут совпадать, т.е.
![$X_{i}[p]=X_{j}[q]$ $X_{i}[p]=X_{j}[q]$](https://dxdy-01.korotkov.co.uk/f/c/9/2/c92dc82fb23bb7c2abaf8ad5b27969d282.png)
, если существует ребро

в биграфе

. Обратное также верно: если
![$X_{i}[p]\neq X_{j}[q]$ $X_{i}[p]\neq X_{j}[q]$](https://dxdy-04.korotkov.co.uk/f/b/2/5/b252a5e1519e17efc422999c98b380c782.png)
, то не существует ребра

в биграфе

. Каждая из вершин

в биграфе

будет инцидентна только одному ребру (и это ребро

), так как в силу формулы (5) версии 2 препринта:

(ha предложил уточнение для верхней границы

, однако в данном случае это не принципиально).
Из (5) также видно, что все

.
Пусть функция

возращает трансверсаль (подмножество ребер биграфа

), если такая трансверсаль существует (любую трансверсаль, если их несколько), и пустое множество в противном случае.
Алгоритм. 1) Для указанной на входе пары вершин

построим биграф

, как описано выше.
2) Будем перебирать все его ребра за исключением ребра

, для каждого ребра

построим биграф

, как описано выше. Если

, то меняем ребра

, иначе удаляем ребро

из

.
3) Если

, то полученная трансверсаль будет единственной, и она будет представлять изоморфное отображение заданных графов.
Конец алгоритма.
Докажем корректность алгоритма. При этом будем считать, что на входе задана пара подобных вершин. Доказательство разобъем на четыре достаточно независимых друг от друга части.
1) Прежде всего покажем корректность постановки задачи об общих представителях. (В тривиальных хрестоматийных случаях такое доказательство является зачастую излишним, поскольку в задаче о браках, например, то, что различные представители являются действительно представителями, а не посторонними персонами, следует из условия самой задачи.) Итак, веса всех вершин линейно зависимы от начальных весов всех вершин, т.к. все

. Поэтому любое уравнение СЛУ накладывает одинаковые по жесткости условия на распределение весов (по Свойству 2 суммы начальных

и конечных весов равны, поэтому речь идет о перераспределении начальных весов). (Например, если бы какое-то

, то по

-ому уравнению СЛУ величина

не зависела бы от начального веса вершины

.) Поэтому, пользуясь терминологией теории распознавания образов, можно утверждать, что во всех уравнениях все признаки

одинаково информативны. И поэтому в пространстве данных признаков (весов) любая вершина графа

может быть представителем всех вершин этого графа или изоморфного ему

. Это очень важный, хотя и не очевидный момент, поэтому, хотя "лирические'' отступления не приняты в доказательствах, но в данном случае по причине неочевидности такое отступление выглядит уместным. Еще в прошлом веке журнал Scientific American опубликовал впечатляющую корреляцию рождаемости в одной из скандинавских стран от поголовья аистов, тем самым проиллюстрировав, насколько больной является практическая проблема выявления действительных (а не мнимых) зависимостей. В нашем случае существует строгая очевидная зависимость. Без такой зависимости содержательная постановка вопроса об общих представителях была бы некорректной.
Отметим также, что для вершин с равными степенями

(препринт версия 2, формула 6) и, как уже отмечалось, все

. Поэтому, если вершина

подобна вершине

, а вершина

подобна вершине

,

, то для каждой вершины

найдется такая вершина

, что ребро

и

и таким образом

.
2) Докажем, что если

, то эта полученная в результате работы алгоритма трансверсаль будет единственной. Как было отмечено выше: каждая из вершин

в биграфе

будет инцидентна только одному ребру

. Поэтому в пересечении

для вершин

останется только это ребро, и при замене ребер

в биграфе

вершины

будут инцидентны только одному ребру

. Перебрав все ребра
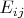
, мы получаем биграф

, в котором каждой вершине инцидентно только одно ребро.
3) Докажем, что если в результате работы алгоритма

, то она будет представлять изоморфное отображение заданных графов. Как было отмечено выше:
![$X_{i}[p]=X_{j}[q]$ $X_{i}[p]=X_{j}[q]$](https://dxdy-01.korotkov.co.uk/f/c/9/2/c92dc82fb23bb7c2abaf8ad5b27969d282.png)
, если существует ребро

в биграфе

. При этом

будет общей для
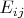
и для

, т.е. для каждого ребра

найдется ребро

. Возьмем перестановку

, заданную этими ребрами (т.е. для каждого ребра

полагаем

) и

линейно независимых векторов

. Пусть

, тогда получим

и по Утверждению 3

будет изоморфизмом.
4) Пусть порядок перебора первых

ребер биграфа

совпал с отображениями, дающими изоморфизм графов:

. Тогда

будет общей для

. Пусть далее в переборе следует ребро

, образованное парой неподобных вершин

, таких, что

. Тогда

, иначе

было бы общей для

и существовал бы изоморфизм, в который бы входило отображение

, а тогда бы вершины

были бы подобны, что противоречит сделанному выше условию. Пусть далее в переборе следует ребро

, образованное парой подобных вершин

. Если

, то будет найден другой изоморфизм, иначе ребро

будет удалено. В силу свойств коммутативности и ассоциативности операции пересечения, результат не зависит от порядка перебора ребер биграфа

.
Конец доказательства корректности алгоритма.
Из доказанного следует, что задача изоморфизма графов может быть сведена к частному случаю задачи поиска общих представителей.
Работа алгоритма для неизоморфных графов и неподобных вершин на его входе не рассматривается, поэтому результат должен быть проверен функцией Verify. Очевидно, что подавая на вход алгоритма пары вершин

, в случае изоморфных графов, мы натолкнемся на пару подобных вершин, для которых алгоритм сработает доказанным выше образом. В случае неизоморфных графов возможны непредсказуемые результаты, все они будут забракованы функцией Verify. Как было отмечено выше, число ребер

не превосходит

, следовательно, число биграфов

не превосходит

. Построение каждого биграфа имеет полиномиальную вычислительную сложность. Следовательно, алгоритм закончит работу за полиномиальное время. Алгоритм можно модифицировать, добавив условие выхода из шага 2, как только будет найдено

биграфов с общей трансверсалью. Однако оценку сложности для наихудшего случая такая модификация не улучшит.