Приходится рассмотреть много случаев отдельно. Рассмотрим для произвольного простого числа р все возможные реализации периода. Отдельно рассмотрим малые простые значения.
р=2, с=0. Последовательность

- период 2.
р=2, с=1. Последовательность

- период 3.
р=3, с=0. Последовательность

- период 4.
р=3, с=1. Последовательность

- период 6.
р=3,с=2. Последовательность

- период 3.
р=5, с=0. Последовательнотсь

- период 4.
р=5,с=1. Последовательность

- период 6.
p=5,c=2. Последовательность

- период р=5.
р=5,с=3=-2. Последовательность

- период 2р=10.
р=5,с=4. Последовательность

- период 3.
Как видно, уже при p=2,c=0 не выполняется условие задачи.
Общий случай

. Характеристическое уравнение

. Решение

с=2. Решение

- период р.
с=-2=р-2. Решение

- период 2р.

- квадратичный вычет по модулю р. Тогда корни из
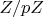
(

) реализуются все случаи (

). Соответственно решение

Период

. Когда

, число
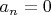
, однако

. Реализуются все делители

большие 2.

- квадратичный невычет. В этом случае корни из квадратичного расширения
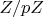
. При этом

. Т.е. период является делителем числа

. Здесь так же реализуется все делители большее 2.
Таким образом утверждение неверное.
Например

- период 5 и не равен периоду по модулю 23 ни при каком

.