Привожу своё, довольно грубое решение.
Для начала выведем формулу для изменения температуры поверхности пластины при попадании на ней воды. Причём перегретой воды.
Все параметры воды обозначаем нижним индексом "w", а тела "sb". Изменение внутренней энергии воды равно

так как вода уже перегрета и при соприкосновении с пластиной испарится почти не меняя температуру. Так же пользуясь тем, что она перегрета опишем её уравнением Менделеева-Клапейрона

, где

молярный объём воды. После чего не трудно видеть, что

и значит

Используя, что

и соответсвенно

можно сказать, что

, где

- плотность водяных паров. И переходя к конечным приращениям можно сказать, что

На такоую же величину измениться и свободная энергия пластины

откуда не трудно заметить, что

Так как данная величина получается отрицательная, что и понятно почему, то в дальнейшем мы будем обозначать

её модуль.
Теперь, когда у нас есть выражение описывающее возникающую разность температур на пластине за одно использование воды опишем процессы происходящие в пластине.
Возникшая разность температур породит тепловой поток

, где

- площадь поверхности одной стороны пластины,

- искомая функция распределения, Q - теплота переносимая потоком,

- коэффициент теплопроводности,

- координата, ну и t - время. Так как функция распределения температуры будет симметрична относительно центра пластины, то введём систему координат так, чтобы 0 был в центре пластины и значения x возрастали к её грани и в точке, где грань заканчивается принимал значение

, и будем рассматривать случай
![$ x \in [0,d] $ $ x \in [0,d] $](https://dxdy-04.korotkov.co.uk/f/7/0/b/70ba16586a6460d3e538de9ce797267182.png)
.
Преобразуем уравнение (1)с учетом того, что

где С- теплоёмкость пластины

получим уравнение в частных производных. Решив его - получим искомую функцию распределения.
(привожу не правильный, но довольно-таки похожий на истину способ сведения этого дифура к обычному дифференциальному уравнению и получению из него искомой функции)
Подчёркиваю,
это не правильное решение. Я сам об этом знаю
Не будем особо задумываться о математике, поэтому скажем, что при
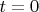
искомая функция

имеет вид

тогда очевидно, что

Где

- температура пластины в центре. Решая эту систему получим, что


и соответсвенно

Переобозначая

предположим, что

, тогда не трудно заметить, что


и подставляя это в уравнение (2) получим

обыкновенное дифференциальное уравнение с разделяющимися переменными.


(Оффтоп)
Я надеюсь вы меня простите за то, что я не стал это всё полностью преобразовывать

И тогда

Подчерку ещё раз, что
этот способ очевидно не правильный, но довольно-таки похожий на правильный.
