Число транспозиций вектора с заданным условием

[Mathemt]

Привет, форумяне!

Задачка, честно говоря, не олимпиадная, но вполне может быть такой - скажем, на олимпиаде по перечислительной комбинаторике. Постановка задачи такова:

В N-мерном пространстве задан вектор А. Все компоненты - натуральные числа, причем некоторые из них могут совпадать. Над вектором А определена операция транспозиции А -> Transpose(А), т.е. перестановка его компонент.

Задан линейный функционал: F(А) = (А, W) (скалярное произведение), где W – некоторый фиксированный вектор, все компоненты которого также являются натуральными числами.

Найти число разных транспозиций вектора А, таких, чтобы F(Transpose(А)) = F(А).

Понятно, что уже при N>10 тупой перебор вариантов на компе получается утомительным. Вполне удовлетворила бы асимптотическая формула, дающая решение с точностью порядка процентов, можно даже десятков процентов.

Если эта задача слишком сложна, буду рад услышать о конкретном источнике, в котором можно найти попытки ее решения. Заранее прошу прощения за то, что не воспользовался тегом Math. Кажется, формулы и так понятны...

[maxal]

Скорее бесполезное наблюдение (хотя кто знает):
если $A=(a_1,\dots,a_n)$ и $W=(w_1,\dots,w_n),$ то искомое число перестановок компонент вектора $A$ равно коэффициенту при $x^{F(A)}y^{2^n-1}$ в разложении

$$f(x,y) = \prod_{i=1}^n \sum_{j=1}^n x^{a_j w_i} y^{2^{j-1}},$$

а также (в виду симметрии) в разложении

$$g(x,y) = \prod_{i=1}^n \sum_{j=1}^n x^{a_i w_j} y^{2^{j-1}}.$$

Добавлено спустя 5 минут 22 секунды:

Можно попробовать вычислить этот коэффициент приближенно по интегральной формуле Коши, используя методы численного интегрирования, но точность такого подхода я не берусь оценить.

[Mathemt]

Спасибо, maxal. Не ожидал столь быстрой реакции. Ваш ответ великолепен по точности, без иронии.

Хорошо, что я догадался упростить постановку задачи. В первоначальном варианте компоненты векторов не были целочисленными, да и сама точность равенства скалярных произведений была не абсолютной. Но в действительности оба упрощения не слишком существенны, так как задача легко сводится к целочисленной без потери точности, а точность соблюдения равенства - просто дань традиции в век машинных алгоритмов.

maxal, Вы не могли бы указать источник, который можно было бы почитать, чтобы понять, откуда взялась эта производящая функция и что с ней делать для получения конечного решения?

[maxal]

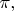
Это не совсем производящая функция, так как нас в ней интересует всего лишь один конкретный коэффициент. В общем виде можно показать, что коэффициент при $x^m y^{2^n-1}$ в разложении $f(x,y)$ равен числу перестановок $\pi,$ для которых $F(\pi\cdot A)=m.$ Начать можно с того наблюдения, что для получения $y^{2^n-1}$ из каждого множителя в $f(x,y)$ должен быть выбран свой уникальный $j,$ так что все эти выбранные $j$ образуют множество $\{1,\dots,n\}.$ Это следует из того, что показатель $2^n - 1 = 2^0 + 2^1 + \dots + 2^{n-1},$ возможно с перестановкой слагаемых, но никак иначе. Поэтому выбранные таким образом степени $y$ гарантируют выборку "перестановочных" произведений (т.е. $y^{2^{j_1-1}}\dots y^{2^{j_n-1}},$ где $\{j_1,\dots,j_n\}=\{1,\dots,n\}$) из всех возможных, в то время как степени $x$ "вычисляют" скалярное произведение на этих перестановках.