Так как мой вопрос не лучше ли определять выполнимость формулы

на совокупности последовательностей вместо последовательности не вызвал комментариев, то мне пришлось разбираться с этим самому. Мои соображения «выдаю» в два приема.
Сначала Мендельсон разъясняет, что такое предикатная буква

и дает примеры


и т. д. Пишет, что «Верхний индекс предикатной или функциональной буквы указывает число аргументов, а нижний индекс служит для различения букв с одним и тем же числом аргументов.» Затем «Предикатные буквы, примененные к термам, порождают элементарные формулы, ...

— элементарная формула.» И после ещё ряда определений переходит к индуктивному определению «... что значит, что формула

выполнена на последовательности

из
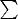
при данной интерпретации.»
В определении четыре индуктивных шага. Первые три говорят о выполненности тех или иных формул при подстановке символов, представляющих элементы последовательности на места свободных вхождений предметных переменных. А четвертый шаг я уже цитировал: «(iv) Формула

выполнена на

тогда и только тогда, когда формула

выполнена на любой последовательности из

, отличающейся от

не более чем своей
i-й компонентой.» Я не стал бы цитировать это предложение опять, если бы не комментарий, резюмирующий эти четыре шага, немедленно следующий за ним: «Иначе говоря, формула

выполнена на последовательности

тогда и только тогда, когда подстановка при каждом

символа, представляющего

на места всех свободных вхождений

в

приводит к истинному в данной интерпретации предложению.» Этот комментарий по отношению к четвертому шагу можно «прокомментировать» известной фразой «Вас здесь не стояло».
Но нестыковки только начались. Дальше идут следствия из этого определения. И среди них следствие «(VII) Всякий частный случай всякой тавтологии истинен во всякой интерпретации.» А откуда здесь взялись тавтологии? У нас формулы, выполненные или нет, на некоторой последовательности в данной интерпретации. А тавтология это: «Пропозициональная форма, которая истинна независимо от того, какие значения принимают встречающиеся в ней пропозициональные буквы, называется тавтологией.» Страница 24. Дело, конечно, можно поправить, если объявить предикатной буквой символ

Но я именно по этому и показал, что у Мендельсона

начинается с

Т. е. в формулы исчисления предикатов хорошо бы включить и пропозициональные формы (так, мне кажется, и делают ряд авторов. Не ошибаюсь?) т. е. высказывания. Интересно, что ряд высказываний является формулами по определению -- это формулы с только связанными переменными. Но, если некоторые пропозициональные формы (тавтологии) истинны в любой интерпретации, то возникает вопрос, а есть ли формулы с только связанными переменными истинные в любой интерпретации? Об этом чуть позже.