
В общем случае зависимость

от

не будет функциональной, поскольку, если
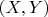
удовлетворяет системе, то и

удовлетворяет системе, где


- образующие по модулям

,

,

- натуральные.
Можно систему переписать так:

Выражая

из 1-го и подставляя во 2-е, получим уравнение

. Подставляя произвольное

можно получить довольно много решений при произвольных

с помощью алгоритма Евклида.
Задание не очень естественно выглядит. Откуда такое взялось?
