Теория вероятностей: распределение случайной величины

[Selius]

Есть задача:
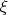
Найти распределение случайной величины $ \eta = \frac{\xi}{2} \left( 1 - (-1)^\xi \right) $, если $ \xi $ имеет геометрическое распределение.

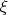
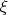
Сам додумался лишь до того, что в зависимости от чётности $ \xi $, $ \eta $ будет обращаться то в ноль, то в $ \xi $. Можно ли судить по этому, что $ \eta $ также имеет геометрическое распределение?
Если же рассуждения неверны, то натолкните, пожалуйста, на верный путь или посоветуйте, что можно почитать, чтобы разобраться.

[ИСН]

Смотря что называть геометрическим распределением. Ну, с какой вероятностью $\eta$ будет равна 0? А 1? А 2? Вообще, где все формулы? У Вас же не словесное описание спрашивают (типа "распределение было какое-то приплюснутое и скошенное вправо"), а формулы.

[Selius]

ИСН в сообщении #443874 писал(а):

У Вас же не словесное описание спрашивают (типа "распределение было какое-то приплюснутое и скошенное вправо"), а формулы.

Мда, ну значит глупость сказал, думал, что нужно просто как-то классифицировать...

Я знаю, что функция вероятности для геометрического распределения
$ P \{ \xi = n \} = q^n p $
, где $ p $ — вероятность успеха, а $ q $ — вероятность неудачи.

Проблема в том, что я не знаю, какие нужно сделать преобразования, чтобы найти распределение $ \eta $. То есть, хотелось бы разобраться, с какой стороны вообще подойти к задаче?

[ИСН]

ИСН в сообщении #443874 писал(а):

Ну, с какой вероятностью $\eta$ будет равна 0?

[Selius]

Эмм, ну как бы сказать... Ну:
$ P \{ \eta = 0 \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 0 \} = P \{ \xi - \mbox{чётное} \} $
Я понимаю, что это не то, но ни на что больше меня этот вопрос не наводит.

[ИСН]

Почему не то. Именно то, только теперь подставить бы их явный вид и свернуть.
Потом

ИСН в сообщении #443874 писал(а):

А 1? А 2?

[Selius]

$ P \{ \eta = 1 \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 1 \} = P \{ \eta = 1 \} = (1 - p) p = p - p^2; $

$ P \{ \eta = 2 \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 2 \} = 0 $ — и также для всех $ \eta = 2 m; \; m = 1, 2, \ldots; $

А вот про явный вид не понял. Можно чуток подробнее?

[ИСН]

Ну, вот $p-p^2$ - это явный вид. А $P\{\xi - \mbox{чётное}\}$ - нет. Ну и если Вы уже описали все чётные от 2 и выше, то опишите все нечётные (и 0) - всё это вместе и будет ответ.

[Selius]

Получается как-то так, правда насчёт последнего не уверен:
$ P \{ \eta = 2m \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 2m \} = 0; \; m = 1, 2, \ldots; $
$ P \{ \eta = 2m - 1 \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 2m - 1 \} = P \{ \xi = 2m - 1 \} = $
$ = (1 - p)^{2 m - 1} p; \; m = 1, 2, \ldots; $
$ P \{ \eta = 0 \} = P \{ \frac{\xi}{2} \left( 1 - (-1)^{\xi} \right) = 0 \} = P \{ \xi - \mbox{чётное} \} = \sum\limits_{m = 0}^{\infty} (1 - p)^{2m} p; $
Правильно?

[ИСН]

Сумма сворачивается в конечное выражение, а так вроде всё верно.

[Selius]

ИСН в сообщении #444620 писал(а):

Сумма сворачивается в конечное выражение

Ага, $ \sum\limits_{m = 0}^{\infty} (1 - p)^{2m} p = \frac{1}{2 - p} $.

Спасибо большое за помощь!