Исследовать асимптотическую динамику поведения подопытного животного, которое должно приспособиться к действиям экспериментатора, размещающего случайным образом пищу в одной из кормушек: в правую пища кладется с вероятностью

, а в левую - с вероятностью

. Животное после очередного размещения пищи имеет возможность попасть только в одну из кормушек по своему выбору. Следует принять, что стратегия выбора животным кормушки может быть описана детерминированным конечным автоматом с тремя состояниями

: -1,1,2. При

животное бежит в правую кормушку, а при

- в левую. Смена состояний

определяется тем, нашло животное пищу или нет.
Переходы при удаче и ниже Переходы при неудаче
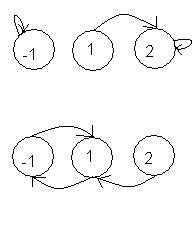
Определить, при каких значениях

вероятность получения животным пищи (при длительно повторяющихся экспериментах) окажется больше значения

--------------------------------------------------------------------------------------------------------------------
построил граф с 6 вершинами типа

, где

,а

(находит, не находит)
составил матрицу 6 на 6 , добавил условие нормировки, получил отрицательную

(всё выражал через

), транспонировал матрицу снова попытался найти неподвижную точку получил вектор с компонентами из

вот не знаю, правильно ли последнее, наверно должно зависеть от

или я чего-то не понимаю? и можно ли сделать всё на графе с тремя вершинами?
-- Сб апр 30, 2011 23:10:17 --извините за граф картинкой)