Идея правильная, но разложения в обеих скобках ошибочны - в степени возводится

и
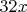
, а не

.
Всё перемножать не требуется - нужен ведь только коэффициент при

.
Неравенства, вызвавшее у Вас подозрения - это просто условие сходимости геометрической прогрессии.