Назовём элементарной теорией множеств, совокупность формул, записанных с участием переменных

, обозначающих множества, символов логических связок, а также символов

,
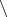
,

,

,

,

,

(символ универсального множества),

.
Существует алгоритм, который, по любой такой формуле отвечает верна она всегда или нет.
Например, можно свести проверку к составлению таблицы истинности. Я выражаю существание такого алгоритма фразой "элементарная теория множеств разрешима" (пусть меня поправят, если что-то некорректно).
Рассмотрим теперь элементарную топологию. Так назовём совокупность, формул, записанных с участием переменных

, обозначающих подмножества некоторого топологического пространства, символов логических связок, теоретико-множественных операций, символа

, обозначающего топологическое пространство, в котором всё происходит, а также символов

(замыкание),

(внутренность),

(граница).
Существует ли алгоритм, который по любой такой формуле отвечает, верна она в общем случае или нет?
-- Пт апр 01, 2011 18:12:05 --Например, верна ли формула

? Или, например,

?