Прошу прощения, я допустил опечатку. Так может быть, что n_{max} равен n.
sup писал(а):
... что происходит, когда концентрация

приближается к

. Согласно Вашей формуле поток вроде как стремится к бесконечности.
А вопрос к
uxikarу:
Какой же физический смысл это имеет?
1) все второе краевое условие - это закон сохранения масс для тонкого пограничного слоя, охватывающего частицу. 2) кол-во молекул, прилипших к поверхности выражается через кол-во молекул в жидком слое.
Если n_{max}=n, то все места на поверхности заняты и, я так понимаю, либо наступит полное равновесие, либо поменяется направление диффузионного потока и молекулы будут отлетать от поверхности, хотя последнее, наверное, может быть только если добавить температурные изменения.
По идее у фильтров ограниченный срок годности, потом если только разогревом восстанавливать.
А Вы можете выписать нужную систему? Без всяких упрощений. Вот уж если она окажется "неподъёмной", тогда и будем упрощать.
Наверное надо отказаться от "одномерщины" и сразу же написать оператор Лапласа. Может там еще какие-то слагаемые есть?
Можно сделать, например так:


Для обоих уравнений поставить те же граничные условия:

На концентрацию условия не изменять на поверхности, а для температуры почти то же самое



.
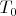
и

- начальные температура и концентрация.
Константы должны быть все положительны.
То, что вошло в частицу то вышло из реактора, а интерес составляет как раз то что там творится. Надо еще добавить закон сохранения масс, в который будет входить n и n_{b} (из краевого условия уравнения диффузии).
Над лапласом в сферических координатах я подумаю. Но если это все записать - кошмар получится.
-- Вт мар 29, 2011 23:24:13 --sup Но усложнять мне нельзя ! Мне существование\единственность доказать надо. Я так и не понял в каком пространстве предсказывается решение и какая идеология выбора этого пространства. Был бы признателен если бы Вы описали шаги и какие результаты могут использоваться.