Не решился пойти прямо к математикам :) Зачем нам дифуры?

[LynxGAV]

Потому что в данном примере уравнения решаются численно (а не аналитически). Посмотрите какие-нибудь учебники по этому поводу.. Очень доходчиво объяснено, например, в "Numerical methods for engineers" Chapra, Canale в разделе Ordinary Differential Equations. Я проинтегрировала в Mathematica. Картинка получилась идентичная.

Если хотите, возьмите за основу сии строки и просто их модифицируйте для своего случая:

r1 = 1/100; r2 = 1/100; k1 = 100; k2 = 200;
eq1 = x'[t] == r1*x[t]*(1 - (x[t] + y[t])/k1)
eq2 = y'[t] == r2*y[t]*(1 - (x[t] + y[t])/k2)
iv1 = x[0] == 20; iv2 = y[0] == 1;
sol = NDSolve[{eq1, eq2, iv1, iv2}, {x[t], y[t]}, {t, 0, 2000}, Method -> ExplicitRungeKutta, MaxSteps -> 50000];
eval1 = Evaluate[x[t] /. sol]; eval2 = Evaluate[y[t] /. sol];
g = Plot[{eval1, eval2}, {t, 0, 2000}, PlotPoints -> 20000, PlotStyle -> {Hue[0], Hue[0.3]}, PlotRange -> All, AxesLabel -> {"t", "x,y"}];
Export["a.bmp", g, "BMP", ImageSize -> 200, ImageResolution -> 200]

И все-таки обратите внимание на важность выбора временной шкалы для получения разумных результатов. В базовой модели авторы все параметры рассчитывали на год, потому и временная шкала соответствующая. Не имеет смысла рассматривать естественную смертность деревьев в штуках на день, это же не помидоры.. Может этот параметр у Вас не будет играть роли, но будут другие.

Уравнения решаются численно иногда из удобства, но очень часто, потому что аналитическое решение найти не возможно. Стандартный метод Рунге-Кутта 4-го порядка дает достаточную точность, но есть и более продвинутые. В общем все подобные системы элементарны..

Добавлено спустя 24 минуты 4 секунды:

Alifer писал(а):

Спасибо огромное за доходчивое объяснение, хорошая получилась бы статейка для начинающего Ботаника .

Признаться честно, первый раз в жизни с ботаником общаюсь. У меня, правда, была соседка, которая биофак закончила, но ни о физике, ни о математике, ни о биологии мы с ней не беседовали.



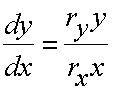
Эх.. Этот метод позволяет найти орбиты.. У Вас есть две неизвестные функции $u,P$ времени $t$ (если один лес), то есть общую картину происходящего Вы можете получить в трехмерном пространстве (ось времени, ось плотности биомассы, ось обобщенного показателя плодородия). Представьте, что ось времени сжали -- пространство стало двухмерным и Вы в фазовой плоскости получите некоторую кривую, соответствующую решению системы. Также можно судить об (асимптотической) устойчивости или неустойчивости решения, характеризовать стационарные точки.

Alifer писал(а):

Может по аналогии мне не достаточно аналогичного численного интегреровая для определения приращения u и P.

Я предлагаю решать численно, дабы не сильно мучаться. И результат-то у Вас будет вполне приличный, если будет правильно составлена система. Тем временем почитывать учебники по дифурам (подходящий "Differential Equations and Their Applications" Martin Braun, раздел "Qualitative Theory of Differential Equations"), если решите проводить еще какой-то анализ.

[Alifer]

LynxGAV писал(а):

Я предлагаю решать численно, дабы не сильно мучаться. И результат-то у Вас будет вполне приличный, если будет правильно составлена система. Тем временем почитывать учебники по дифурам (подходящий "Differential Equations and Their Applications" Martin Braun, раздел "Qualitative Theory of Differential Equations"), если решите проводить еще какой-то анализ.

Значит следуя моим скромным умозаключениям, я могу решить уравнение прироста для u:
u_t:=u_t_-_1 + (k*C_t*V_t-D_t)*u_t_-_1
(который зависит от конкуренции С, интенсивности потребления ресурсов V и смертности D, изменяющихся во времени, и рассчитываемых по другим дифференциальным или обычным уравнениям). Если форма! графика будет отличаться от результатов натурных наблюдений, то можно добавить по смыслу еще какой либо "поправочный " коэффициент или дополнительную функцию, так? И это будет называться численным интегрированием (другие детали, как начальные условия и т.п. пока опустим)?

[LynxGAV]

Alifer писал(а):

Значит следуя моим скромным умозаключениям, я могу решить уравнение прироста для u:
u_t:=u_t_-_1 + (k*C_t*V_t-D_t)*u_t_-_1

В свою очередь, из моих скромных умозаключений могу только догадываться, почему у параметров появился индекс $t$.

Цитата:

изменяющихся во времени..

Вы наверное не совсем поняли, что сделали. По-перше, система стала не автономной, в ней фактически в явном виде появилось время (ее можно опять привести в нормальному виду, но кому это надо?), если задана функциональная зависимость. По-друге, она может оказаться нелинейной, что не хорошо (но и не плохо, потому что линейные системы ничего интересного не дают).

Начнем с полуначала..

Цитата:

рассчитываемых по другим дифференциальным или обычным уравнениям

Что еще за уравнения? Коэффициенты вы должны отобрать из экспериментов. Исследуете на предмет удобрений -- 1. положити х единиц в почву -- замерили рост, 2. положили х+1 единицу в почву -- растет еще лучше, 3. положили х+2 единицы -- рост меньше, чем в случае 2, то бишь случай 2 как будто бы оптимальный и коэффициент, он же параметр в этом случае постоянен. Далее проводите эксперименты с другими коэффициентами. Идельно еще измерить имеются ли корреляции между параметрами. То есть при х единиц удобрения и влажности gav+3 рост может быть такой же как и при х+2 и gav+1. Понятно?

Цитата:

Если форма графика будет отличаться от результатов натурных наблюдений, то можно добавить по смыслу еще какой либо "поправочный" коэффициент или дополнительную функцию, так?

Если она у Вас не будет отличаться, я сильно удивлюсь . Поймите, что Ваше насаждение -- это не хвойный лес и не обязано подчиняться уравнениям, его описывающим. Но это отнюдь не значит, что Вы не можете заимствовать идеи/уравнения/части уравнения из работ, которые читаете в интернете. Что-то среди перечисленных Вами параметров не встретила ни одного, упоминавшегося в базовой модели (но у них есть параметры, которые учесть необходимо, -- как естественная смертность и др. читайте внимательно). В конце концов кто из нас биолог или ботаник и должен понимать важность эксперимента в моделировании?

Цитата:

И это будет называться численным интегрированием (другие детали, как начальные условия и т.п. пока опустим)?

Вы составили систему уравнений -- аналитическую, в которой параметры записали буквами (х, у, gav и т.п.) Далее у вас два пути -- 1. система получилась симпатичная, линейная или просто решаемая аналитически. Тогда из общего решения (функции времени), используя конкретные начальные условия и конкретные значения параметров, которые Вы отобрали, получаете частное решение и смотрите как оно согласуется с исследованиями. 2. система аналитически не решаемая. Тогда подставляете численные значения параметров, решаете задачу Коши и получаете, на этот раз численно, функции времени соответствуете частному случаю.

Alifer, я начинаю уставать.. Пожалуйста, прикладывайте больше усилий .

[Alifer]

Спасибо уважаемая LynxGAV за потраченное время и помощь. Я прямо и не ожидал столь развернутого ответа. Докачиваются книги . Будем читать.

[LynxGAV]

Alifer писал(а):

Спасибо уважаемая LynxGAV за потраченное время и помощь. Я прямо и не ожидал столь развернутого ответа. Докачиваются книги . Будем читать.

Давайте без приставок к никам.. Это все вещи достаточно элементарные и при прочтении литературы Вам не понадобятся никакие советы. Если что -- на форуме рано или поздно кто-то отзовется .

[Alifer]

Мда, смешно иногда перечитывать свои вопросы, особенно по прошествию какого-то времени.
Начав свой опус, нехотя хотелось бы его продолжить, возможно коллега-студент почерпнет для себя что-либо.
Являясь человеком достаточно ленивым по своей натуре, я собрался не понять, а «взять» эти ДУ напором, измором. Перечитывая литературу, я не обращал внимания на весьма очевидные факты, а пытался найти «ТО», по прочтению чего меня озарит и в мгновение ока пойму все тонкости этой удивительной науки. Сложно оценить самого себя со стороны. Все время кажется что тратишь сАмое драгоценное время на переворачивание страниц, а этого «ТО», все нет и нет. Даже в десятый раз перечитывая ответы на свои школьные вопросы я жадно всматривался в буквы… и так хотелось увидеть то, что ждешь, даже абсолютно не понимая чего.
Мне упрямо не хотелось видеть что ДУ имеют какие-то странные отношения с интегрированием и производной. Еще большим открытием для меня стало то, что ДУ это оказывается «СКОРОСТЬ изменения процесса», а совершенно не «скорость изменения ПРОЦЕССА». Этого я не видел даже в ответах на свои вопросы. Как дивно у меня проходят процессы познания.
Как же нам часто не хочется верить в то что так очевидно, но как прискорбно бы это не было, ОСОЗНАВ наконец всю глубину своих незнаний в математике я взял школьный учебник по алгебре и началу анализа. Перечитав его для начала пару раз, открыл для себя много интересного. Как оказывается понятно там пишут. Как приятно вспомнить школьную математику, бывшую некогда так отвратительной. Сколько нового сейчас видно у Гаузе, Ризниченко, Карева и еще дюжины других.
Ваши ответы в какой-то мере помогли мне понять, что именно я не знаю, а чего просто не понимаю.

Пользуясь случаем хотелось бы узнать как быть с одним уравнением. Порывшись очередной раз в литературе нашел пару уравнений:
$${\frac{{d(WS)}}{{dt}}} =P-\frac{{bS}}{R}-\frac{{WkS}}{K+S}
$${\frac{{dW}}{{dt}}} = \frac{{YWkS}}{K+S}
Я пытаюся решить эту систему в Маткаде. Как в данном случае определить S (и тем более указать в матрице начальных условий пер состояния).
Еще дальше есть:
$${\frac{{d(WS/g)}}{{dt}}}?.

[LynxGAV]

Пишите, пожалуйста, что переменные, а что константы. Не все же догадываются, что обозначают все эти буковки.

Сначала распишите производную произведения в первом уравнении и используйте второе уравнение. Таким образом получите уравнение относительно $S$.

[Alifer]

Цитата:

Пишите, пожалуйста, что переменные, а что константы.

Пардон. Переменные - W и S, константы все остальное.

[Alifer]

LynxGAV писал(а):

Сначала распишите производную произведения в первом уравнении и используйте второе уравнение. Таким образом получите уравнение относительно $S$.

Правильно ли я делаю:

$${\frac{{dW}}{{dt}}S}+{\frac{{dS}}{{dt}}W}= P-\frac{{bS}}{R}-Y\frac{{dW}}{dt}

$${\frac{{dS}}{{dt}}}= {\frac{{1}}{{W}}}(P-\frac{{bS}}{R}-\frac{{Y^{2}WkS}}{K+S}-\frac{{YWkS^{2}}}{K+S})

LynxGAV писал(а):

Нет. Проверьте первую строчку, а потом и вторую.

Дабы уж не плодить сообщений поправлю прямо здесь. Надеюсь, что теперь правильно:
$${\frac{{dW}}{{dt}}S}+{\frac{{dS}}{{dt}}W}= P-\frac{{bS}}{R}-\frac{{1}}{Y}\frac{{dW}}{dt}

$${\frac{{dS}}{{dt}}}= {\frac{{1}}{{W}}}(P-\frac{{bS}}{R}-\frac{{WkS}}{K+S}-\frac{{YWkS^{2}}}{K+S})

[LynxGAV]

Нет. Проверьте первую строчку, а потом и вторую.

Добавлено спустя 43 минуты 59 секунд:

Нет уж, редактируйте, пожалуйта, после. И не тяжело, и логическая цепочка прослеживается.

Да, получается $\frac{dS}{dt}=\frac{1}{W}\left(P-\frac{bS}{R}\right)-\frac{kS}{k+S}\left(SY+1\right)$.

Добавлено спустя 49 секунд:

За сообщения, если они по делу, никто не наказывает .

[Alifer]

Цитата:

Да, получается $\frac{dS}{dt}=\frac{1}{W}\left(P-\frac{bS}{R}\right)-\frac{kS}{k+S}\left(SY+1\right)$.

маленькое замечание: в уравнении вместо "k+S" должно быть "K+S".
Красивое получилось уравнение.
Спасибо БОЛЬШОЕ.
-<-@

[Alifer]

Накопал в сети интереснейшую книгу Торнли переведенную в Киеве. В этой книге приведена модель. Здесь интересно записаны уравнения:
производные в первых двух от (V*С), а в следующих четырех (V,С) (для N тоже самое). Это ошибка или так должно быть? И что тогда означает эта веселая запись d(V, C)/dt?

[LynxGAV]

Обычно обозначения поясняются по ходу текста или в начале книги. Также следует исключить вариант замены индексов запятыми при распознавании отсканированного текста.