нда.. действительно не верно, глупости говорю...
Попробуем тогда так:
Есть еще такое утверждение(сразу переформулирую его на нашу сигнатуру): Если для любых

и для любого
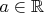
существует автоморфизм

системы

, для которого

и

, то

является элементарным расширением

, т.е. то, что нам и нужно доказать.
Что же значит автоморфизм в нашем случае, что если
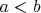
, то

. Пусть для определенности

. Если

из условия теоремы принадлежит

то все тривиально, если же нет, то либо

, либо

либо

Рассмотрим последний случай(остальные рассматриваются аналогично.
Построим автоморфизм следующим образом

для

. По условию

и

в силу плотности порядка существует

такой, что

, тогда положим

. Ну а то, что

и

очевидно.
Вроде все.
Можно было бы, конечно попробовать доказать первое мое утверждение, но что-то не очень хочется
