Здравствуйте, уважаемые математики!
Не могли бы вы помочь разобраться с задачей? Мне её задали по предмету "Некорректные задачи". А заключается она в следующем: на плоскости дан прямоугольник со сторонами a и b. На этом прямоугольнике расположен правильный n-угольник со стороной 1. Вопрос поставлен так: можно ли определить положение этого n-угольника, используя только измерения по горизонтали и вертикали? И если можно, то какое минимальное количество измерений? Ещё дан шаг, равный 2-

Мне не совсем понятен принцип решения, и сначала хотелось рассмотреть более простой вариант - квадрат. (не будем рассматривать случаи, где стороны квадрата параллельны сторонам прямоугольника, или же диагональ квадрата параллельна им). Проведём вертикальное измерение. И, предположим, мы попали в этот квадрат и получили отрезок длины c. Отложим его. после построения этого отрезка мы пока что имеем бесконечно много возможных вариантов расположения квадрата. Проведём второе измерение. Опять же, предположим, что мы попали и получили отрезок длины d. Рассмотрим два случая.
Первый случай - когда обе проведённые прямые пересекают одни и те же стороны квадрата. Можем ли мы в этом случае утверждать, что по этим двум отрезкам можно однозначно восстановить квадрат?... И если можем, то как это нужно доказать?...
Второй случай - если две прямые пересекают разные стороны квадрата. Будет ли тогда достаточно двух измерений? И как доказать, что эти прямые проходят именно через разные стороны, если по условию не полагается измерять какие-либо углы...?
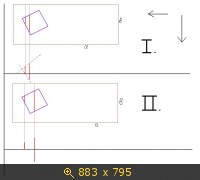
Не до конца понятен смысл этого всего... Буду очень благодарен, если поможете разобраться!
