Пусть

сумма

независимых случайных величин.
Пусть каждая величина

имеет нулевое математическое ожидание
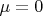
и одну и ту же дисперсию

.
Центральная предельная теорема (ЦПТ) утверждает, что величина

будет распределена приблизительно нормально. То есть вероятность того, что

с некоторой точностью равна

.
Допустим, что какая-то нормально распределенная величина наблюдается в природе.
Предположим что такое распределение возникает в силу ЦПТ.
Значит эта величина представима в виде

.
То есть она складывается из

независимых случайных величин

, каждая из которых имеет отклонение

.
Значит нормально распределенные величины - суммы

величин порядка

. Например, сумма

случайных величин порядка

будет распределена нормально.
Но если же число величин

и их величина

не связаны законом

, то их сумма не будет распределена нормально.
Нет достаточных оснований полагать, что такой закон

обязателен для природы.
Число слагаемых в случайной величине и размер этих слагаемых могут быть какими угодно, и маловероятно что именно такими, чтобы выполнялась ЦПТ.
Значит в природе ЦПТ не применима и нормально распределенных величин в принципе не должно быть.
Поэтому:
знать ЦПТ не надо, изучать не надо, нормальное распределение не нужно, знать его не надо, вся наука (физика, экономика), где нормальное распределение что-то значит, не верна.
Или не так?