Сферическая система координат на индикатрисе

[Time]

Отделено от темы http://dxdy.ru/post420008.html#p420008. АКМ

В.О. в сообщении #418621 писал(а):

Сказали нечто невыразимо прекрасное, но абсолютно недоступное для простых смертных.

Я ж не виноват, что мало кто знаком с финслеровыми пространствами, связанными с коммутативно-ассоциативными гиперкомплексными числами размерности три и выше. А самое удивительное, и не желают дать себе труд познакомиться. Могу Вас заверить, что ничего особенно сложного тут нет. Только непривычно сперва. При желании можете глянуть на статью
http://hypercomplex.xpsweb.com/articles ... /11-04.pdf
непосредственно связанную с обсуждаемым вопросом координатных линий на двумерной сфере трехмерного пространства. Только не евклидова или псевдоевклидова, а специального вида финслерова. Вращения тут гиперболические и образуют абелеву группу. А пара углов на финслеровой сфере (индикатрисе) являются аддитивными параметрами и могут быть представлены внутри экспоненты, как и хотел автор темы, правда, он пытался это сделать в евклидовом пространстве, что принципиально невозможно.

[В.О.]

Углы, характеризующие взаимное расположение двоек, троек и т.д. векторов меня интересуют в связи с неравенствами Белла topic42151.html Но все, что касается БМ и т.п решительно непонятно. Может быть есть какой-то текст на несколько страничек с подробным изложением азов, доступный студенту? Двойные числа и пр.

[Time]

Думаю, в связи с Вашим интересом к неравенству Белла финслеровы пространства с метрической функцией Бервальда-Моора могут оказаться как нельзя кстати. Они на много интереснее и богаче устроены, чем псевдоевклидовы и псевдоримановы пространства, ну разве что, пока еще мало изучены. Именно они, думаю, станут основой новых представлений о геометрии пространcтва-времени. Так что, попробуйте поизучать..

В наиболее простом изложении нужные Вам моменты попробуйте найти в первых трех статьях этого номера журнала:

http://hypercomplex.xpsweb.com/page.php?lang=ru&id=52

Если энтузиазм не пропадет и захотите более полного понимания, почитайте статьи посвященные двойным числам и h-голоморфным функциям от них в другом номере журнала:

http://hypercomplex.xpsweb.com/articles ... ngp_13.pdf

[В.О.]

Спасибо за ссылки. Что-то начинает проясняться, но изложение отрывочное и возникает много вопросов.Например, как из скалярного 3-произведения получить норму вектора? Если в 3-произведение (перманент) подставить один и тот же вектор, то получится норма с лишним множителем 6.
Или еще, Вы считаете количество степеней свободы у двух произвольных векторов в Н3. После нормировки и канонизации остается 2 степени. Вроде, правильно, но и в евклидовом пространстве будет так же. Этим 2 степеням свободы соответствуют два координатных угла в сферической системе координат. Но Вы пишете, что это не так.
Ладно, это технические детали. Надеюсь, когда-нибудь разберусь.

Вот основной вопрос. Если в евклидовом 3-мерном пространстве взять 3 произвольных нормированных вектора, то 3 угла между ними не могут быть произвольными. Они должны удовлетворять некоторым неравенствам (аналогичным неравенствам Белла), которые я, вроде бы, выписал во втором сообщении в topic42151.html
А если взять 3 нормированных вектора в Н3 и бинглы между ними. Могут ли эти бинглы быть произвольными или тоже должны выполняться какие-то ограничения?
В евклидовом пространстве эти неравенства являются критерием евклидовости пространства. Т.е. по ним можно проверять является ли реальное пространство трехмерным евклидовым. По идее аналогичные неравенства (если они возможны) будут проверять реальное пространство на финслеровость .

Является ли финслерово пространство локально евклидовым?

[В.О.]

На последний вопрос ответ отрицательный, конечно.

[Time]

В.О. в сообщении #419303 писал(а):

Что-то начинает проясняться, но изложение отрывочное и возникает много вопросов.Например, как из скалярного 3-произведения получить норму вектора? Если в 3-произведение (перманент) подставить один и тот же вектор, то получится норма с лишним множителем 6.

Ну, так учебники по обычному скалярному произведению почти двести лет шлифуются, а по его скалярному поли- обобщению еще ни одного не написано. Если, правда, таковым не считать единственную на сегодня книгу: Г.И.Гарасько "Начала финслеровой геометрии для физиков", но и там многим изложение покажется отрывочным и неполным. Что поделаешь, издержки всяких начал..

"Лишний" множитель - не помеха. Геометрия не меняется, если метрическую функцию взять с постоянным вещественным коэффициентом.

В.О. в сообщении #419303 писал(а):

Или еще, Вы считаете количество степеней свободы у двух произвольных векторов в Н3. После нормировки и канонизации остается 2 степени. Вроде, правильно, но и в евклидовом пространстве будет так же. Этим 2 степеням свободы соответствуют два координатных угла в сферической системе координат.

В трехмерном евклидовом пространстве вращения имеют не две, а три степени свободы. В четырехмерном - шесть. В четырехмерном же пространстве Бервальда-Моора вращения образуют лишь трехпараметрическую группу. И вращения тут коммутируют друг с другом, в отличии от вращений четырехмерного евклидова пространства.

В.О. в сообщении #419303 писал(а):

А если взять 3 нормированных вектора в Н3 и бинглы между ними. Могут ли эти бинглы быть произвольными или тоже должны выполняться какие-то ограничения?

Конечно же есть свои ограничения и они обусловлены в данном случае уже финслеровой геометрией. Самое же здесь интересное и необычное, отличающее трехмерное бервальд-мооровское пространство от евклидова заключается в том, что кроме длин и углов в нем есть место для еще одного базового геометрического параметра - трингла. В евклиде же тринглов нет, список базовых величин ограничен длинами и углами. Однако с этой особенностью с наскока не разобраться, тем более, что с этими тринглами, не смотря на несколько лет работы и кое какие найденные закономерности еще очень много неясностей.

В.О. в сообщении #419303 писал(а):

Является ли финслерово пространство локально евклидовым?

В обычном смысле, естественно, нет. Скорее уместно сравнивать финслерово пространство с метрикой Бервальда-Моора с таким же по размерности псевдоевклидовым пространством с сигнатурой (+,-,-,...). Однако тут есть нюансы. Но главное тут то, что с точки зрения наблюдателя, для которого одна из неизотропных координат играет роль собственного времени, оставшиеся (n-1) координат при использовании методов хроногеометрии автоматически представляются как почти евклидово пространство. То есть, анизотропию этого пространства, а также иные его неевклидовы свойства довольно трудно обнаружить.. Собственно, именно это и дает надежды на возможность эффективной и непротиворечивой замены псевдоевклидовой метрики пространства-времени на финслерову бервальд-мооровскую.

[В.О.]

Time в сообщении #419423 писал(а):

В трехмерном евклидовом пространстве вращения имеют не две, а три степени свободы

Что-то я вообще перестал понимать. Вот два произвольных вектора в 3-х мерном евклидовом:
$x = (x_1,x_2,x_3)$
$y = (y_1,y_2,y_3)$
У них 6 степеней свободы.
Нормируем оба вектора и фиксируем один вектор. Это эквивалентно тому, что Вы называете канонизацией.
$x = (x_1,x_2,x_3)$
$y = (b_1,b_2,b_3)$
$x^2_3 = 1 - x^2_1 - x^2_2$
$b^2_1 + b^2_2 + b^2_3 = 1$
Остается два свободных параметра $x_1$ и $x_2$.
Эти два параметра можно заменить двумя свободными сферическими углами. Это две степени свободы. Где третья?

Трингл это площадь сферического треугольника на сфере. Аддитивная характеристика тройки векторов. Это написано в первых строках Вашего абстракта.

[Time]

В.О. в сообщении #419508 писал(а):

Это две степени свободы. Где третья?

Третья - во вращении вокруг оси вектора. В трехмерном евклидовом (и псевдоевклидовом) пространстве это возможно, а в трехмерном Бервальде-Мооре - нет.

Просто нужно рассматривать фигуру не из двух, а из трех векторов. Отчасти, такое рассмотрение трех векторов в трехмерном евклиде и бервальд-мооре как раз и показывает возможность существования, кроме длин и углов еще и трингла, но только в финслеровом случае:

http://hypercomplex.xpsweb.com/articles ... /11-01.pdf

В.О. в сообщении #419508 писал(а):

Трингл это площадь сферического треугольника на сфере. Аддитивная характеристика тройки векторов. Это написано в первых строках Вашего абстракта.

Я говорил выше, что с тринглами еще далеко не все ясно. Так, я уверен, что трингл это, и длина вполне конкретной кривой, и площадь конкретного криволинейного треугольника на индикатрисе (но, все же, не сферического), и объем под этим треугольником. За время прошедшее с написания упоминаемой статьи я пришел к выводу, что трингл это тот объект, который в статье не вполне оправданно был назван относительным бинглом. А то, что названо тринглом, является только финслеровым аналогом сферического треугольника, но никак не тринглом. На мой взгляд, критерием правильности того или иного выбора, что именно следует в Н3 именовать тринглом является возможность представления числа из этой алгебры в так называемой лестничной экспоненциальной форме представления. Последняя является очень красивым и естественным (трехэтажным) обощением формулы Эйлера для поличисловых финслеровых пространств, причем она объединяет модуль числа (первый этаж), угол или бингл (второй этаж) и трингл (третий этаж), что называется, в одном флаконе.. Так что, пользуясь случаем, приношу извинения за определенную путаницу, возникшую из-за еще неустановившейся терминологии. К сожалению, не получается продвигаться вперед совсем без ошибок. Иногда болезненных..

[В.О.]

Time в сообщении #419818 писал(а):

не получается продвигаться вперед совсем без ошибок

Да, господи... Не ошибается только тот, кто ничего не делает. Колмогоров и тот делал ошибки.

Time в сообщении #419818 писал(а):

не вполне оправданно был назван относительным бинглом.

С относительным бинглом что-то непонятное. На стр.60 в http://hypercomplex.xpsweb.com/articles ... /11-04.pdf написано "можем определить второй бингл между а и b как длинну дуги единичной окружности, заключенной между некоторой выделенной точкой на этой окружности и найденной выше точкой ее пересечения с геодезической дугой, соединяющей а и b." К евклидову пространству и сферическому углу это вряд ли имеет отношение.
Насколько я понял, в Финслеровом пространстве появляются свободные параметры, характеризующие взаимное положение векторов, по сравнению с евклидовым, и Вы хотите придать им смысл новых углов (инглов). Наверное, это имеет смысл. Но предварительно хотелось бы иметь уверенность, что вся эта тематика имеет, так сказать, глобальный смысл. Есть тут какие-нибудь приложения? Хотя я знаю, что в математике есть множество обобщений, не имеющих никаких приложений.
Если я ничего не путаю, то Вы когда-то говорили, что финслерово пространство может претендовать на роль реального пространства, в каком-то смысле. Это так?

[Time]

В.О. в сообщении #420084 писал(а):

С относительным бинглом что-то непонятное. На стр.60 в http://hypercomplex.xpsweb.com/articles ... /11-04.pdf написано "можем определить второй бингл между а и b как длинну дуги единичной окружности, заключенной между некоторой выделенной точкой на этой окружности и найденной выше точкой ее пересечения с геодезической дугой, соединяющей а и b." К евклидову пространству и сферическому углу это вряд ли имеет отношение.

Я ж и говорю, что постепенно меняю свои представления и сейчас вместо второго (относительного) бингла предпочел бы определить именно трингл. Для последнего, по самой сути этого базового параметра нужны не два, а три вектора, пусть это будет вектор $c$, который для простоты изложения будем считать уже отнормированным по длине, то есть, упирающимся своим концом в индикатрису пространства $H_3$. Тринглом между единичными векторами $(a,b,c)$ можно называть длину дуги единичной (малой) окружности на индикатрисе с центром в конце вектора c и заключенной между точками пересечения этой малой окружности с геодезическими на индикатрисе, проходящими через концы пар векторов $(a,c)$ и $(b,c)$. При таком определении трингл будет пропорционален еще и площади криволинейного треугольника на индикатрисе, ограниченного с одной стороны дугой малой единичной окружности, а с двух других - геодезическими соединяющими концы дуги с вершиной вектора $c$. Также он будет пропорционален объему под таким криволинейным треугольником. Правда, так определенный трингл не будет независим от перестановки местами векторов $a, b, c$, но может это и к лучшему..

В.О. в сообщении #420084 писал(а):

Наверное, это имеет смысл. Но предварительно хотелось бы иметь уверенность, что вся эта тематика имеет, так сказать, глобальный смысл. Есть тут какие-нибудь приложения? Хотя я знаю, что в математике есть множество обобщений, не имеющих никаких приложений.

Пока с приложениями не густо. Но это, думаю, издержки относительно малых знаний о закономерностях финслеровых пространств. Дело в том, что классическая финслерова геометрия, которой скоро (в 2018 г) исполняется сотня лет, стала развиваться не по самому выгодному и интересному для себя пути, а именно в отрыве от понятия угла, а тем более таких величин как тринглы и пр. полиуглы. В результате из рассмотрения выпали обобщения таких замечательных для физики групп преобразований как финслеровы обобщения конформных симметрий, а также сохраняющих инвариантными тринглы и т.д. Для приложений же, особенно в направлении физики важны именно метрически выделенные группы непрерывных симметрий. А сейчас, получается, неизвестна даже полная классификация симметрий таких простеньких пространств как $H_3$ и $H_4$. 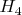Короче, приложения, думаю, дело будущего, которое приблизится, если станет совершенно прозрачной ситуация с полным описанием всех групп нелинейных преобразований имеющих различные метрические инварианты, хотя бы в трех- и четырехмерных финслеровых пространствах связанных с поличислами.

В.О. в сообщении #420084 писал(а):

Если я ничего не путаю, то Вы когда-то говорили, что финслерово пространство может претендовать на роль реального пространства, в каком-то смысле. Это так?

Уже седьмой год подряд проходит международная конференция "Финслеровы расширения теории относительности". В этом году она состоится в Румынии в университете г.Брашов:
http://cs.unitbv.ro/fert2011
Многие физики и математики из числа ее участников полагают, что притязания финслеровой геометрии на роль фундамента будущих представлений о свойствах реального пространства-времени достаточно обоснованны. Правда, есть и много скептиков, вплоть до полного неприятия (это как правило физики, не особенно много времени и сил потратившие на вхождение в тему). Если хотите попробовать составить собственное мнение (а не с чужих слов), советую глянуть доклад C.Кокарева "Алгебраическая единая теория.." на конференции 2010 года. Ссылку на видео Вы найдете на странице:
http://polynumbers.ru/section.php?lang=ru&genre=75
Там же, если захотите, скачайте популярные фильмы о финслеровой геометрии и другие доклады на аналогичную тему.
Доклад Кокарева посвящен простейшим случаям, сводящимся к задачам с двумя независимыми измерениями, но из принятой в нем логики вполне понятно, как двигаться к трех и четырехмерным физически ориентированным теориям на основе геометрий тройных и четверных гиперкомплексных чисел.

[В.О.]

Time в сообщении #420102 писал(а):

Тринглом между единичными векторами можно называть длину дуги единичной (малой) окружности на индикатрисе с центром в конце вектора c и заключенной между точками пересечения этой малой окружности с геодезическими на индикатрисе, проходящими через концы пар векторов и .

Мне совершенно непонятно происхождение такой конструкции.

Может быть, окажется полезным еще одно соображение.
Длина вектора есть аддитивная величина если векторы коллинеарны.
Угол между двумя векторами есть аддитивная величина, если три вектора компланарны.
Трингл ... ?

[Time]

В.О. в сообщении #420856 писал(а):

Мне совершенно непонятно происхождение такой конструкции.

С углами, согласен, проще. Даже с гиперболическими и с финслеровыми. У них по крайней мере есть наглядные аналоги в понятном нам евклидовом пространстве. У тринглов наглядных аналогов нет, поэтому опираться приходится лишь на логику и экстраполяцию свойств длин и углов. Оправданность тринглов еще долго будет оставаться не очевидной, особенно если не появятся их приложения к конкретным физическим задачам.

В.О. в сообщении #420856 писал(а):

Может быть, окажется полезным еще одно соображение.
Длина вектора есть аддитивная величина если векторы коллинеарны.
Угол между двумя векторами есть аддитивная величина, если три вектора компланарны.
Трингл ... ?

Можно и таким образом экстраполировать. Ваше предложение, думаю, можно продолжить так..
Трингл между тремя векторами (в финслеровом пространстве с четырьмя и более измерениями) есть аддитивная величина, если четвертый вектор (с использованием которого появляется складываемый второй трингл) обладает определенным положением к первым трем (тут нужно придумывать специальный термин типа коллинеарности и компланарности). В трехмерном пространстве все вектора будут обладать таким свойством для аддитивности тринглов, как компланарны все вектора двумерного пространства.

Хочу отметить еще раз, что тринглы интересны не сами по себе, а в связи с теми преобразованиями финслерова пространства, которые оставляют их инвариантными. Такие преобразования должны автоматически образовывать множество более широкое, чем изометрические и конформные преобразования рассматриваемого пространства, но не произвольные. Если бы в финслеровых пространствах не было тринглов, у этих пространств не было бы не единого шанса заменить когда ни будь собой пространство-время Минковского для физики, хотя бы потому, что группа изометрических и конформных симметрий этих пространств слишком просты и специфичны, что бы заменить собой общепризнанные группы физически понятных групп симметрий Лоренца и Пуанкаре.

[В.О.]

В определении угла, кажется, есть один неприятный момент. Угол Вы определяете как длину геодезической между концами единичных векторов http://hypercomplex.xpsweb.com/articles ... /11-04.pdf В $\mathbb{R}_n$ при таком определении все нормально и угол не превышает $2 \pi$. Теперь посмотрим в $H_3$. Пусть $A = (1,1,1), B = (b_1, b_2, b_3), \left|B\right| = (b_1 b_2 b_3)^ {\frac 1 3} = 1$
По формуле (33)
$\Phi(A,B) = \left[\ln b_1 \ln b_2\ln b_3 \right]^{\frac 1 3}$
Теперь выберем $b_1, b_2, b_3$ так, чтобы $\Phi(A,B) = 2\pi $. Вроде, ничто не мешает это сделать.
По идее, если $\Phi(A,B) = 2\pi $ то А = В. Но это не так.

[Time]

Вы забываете, что пространства $H_n$ являются многомерными расширениями псевдоевклидовой, а не евклидовой плоскости. На первой, в отличие от второй, угол не является периодической величиной и изменяется от минус до плюс бесконечности. Тоже самое и в $H_3$. Рассмотрите подробнее пространство $H_2$, оно же псевдоевклидова плоскость. А потом сравните с $H_3$. Увидите, все встанет на свои места..

[В.О.]

Хорошо, неограниченность угла можно пережить. В конце концов, при обобщении какие-то свойства угла могут потеряться. Но тут есть еще одна неприятность.
Угол, по своему исходному смыслу, это характеристика взаимного расположения двух векторов. Но в Н3 угол между двух фиксированных векторов зависит от системы координат. Т.е. получается, что в Н3 угол это характеристика взаимного расположения не только пары векторов, но и координатных ортов.