Пусть Е—метрическое пространство. Обозначим через О множество непустых открытых подмножеств Е. Наша игра устроена так.
На шаге 1 игрок 1 выбирает

.
На шаге 2 игрок 2 выбирает

с единственным ограничением
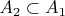
... .
На шаге t игрок (1, если t нечетно, и 2, если четно) выбирает

с единственным ограничением

и так до бесконечности.
Скажем, что игрок 1 выигрывает, если пересечение всех

не пусто.
Если это пересечение пусто, то скажем, что выигрывает игрок 2.
1) Докажите, что если Е полное метрическое пространство, то игрок 1 может гарантировать победу.
2) Докажите, что если E = Q, то игрок 2 может гарантировать победу.
3) Для любого ли Е наша игра имеет цену?
Даже не знаю с чего начать. Буду признателен любым идеям.