Распределение и дисперсия

[Joker_vD]

А вы введите искусственные ограничения $p_i \geqslant \varepsilon_i > 0$.

[PAV]

orsobruno в сообщении #413324 писал(а):

как найти ряд распределения случайной величины, зная соответственно значения случайной величины (x1,..,xi), чтобы удовлетворялись 2 условия:
1. значения всех вероятностей p(xi) > 0
2. Дисперсия минимальна

Это математически невозможно

-- Вт фев 15, 2011 20:48:01 --

Тут могут возникать еще и другие подвохи прикладного характера. Основной - это возможная нечистота используемого датчика случайных чисел. В частности, внутри себя датчик может содержать некоторые дискретные составляющие, поэтому он может быть нечувствительным к чрезвычайно малым колебаниям значений вероятностей. Например, Вы даете ему настолько малую вероятность, что для него это то же самое, что и ноль, и на практике он соответствующее значение просто не выдаст никогда. Возможно, в этом тоже может оказаться причина возможных отклонений. Можете попробовать подсчитать частоты значений, которые выпадают в Ваших опытах, и сопоставить их с заданными изначально вероятностями. Может быть, обнаружится какая-то систематическая погрешность.

-- Вт фев 15, 2011 20:53:24 --

Не забывайте еще и про такой аспект: среднее арифметическое будет близко к математическому ожиданию только при большом числе опытов. Однако "большое число" - это понятие не абсолютное, а относительное. Вам может казаться, что 100000 - это очень много, однако в действительности большим должно быть не число опытов $N$, а ожидаемые количества появлений и непоявлений событий, то есть величины $Np$ и $N(1-p)$. 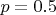Скажем, для правильной монеты с $p=0.5$ количество опытов порядка нескольких сотен - это вполне изрядно, однако для значений $p$ порядка $0.001$ или $0.999$ этого количества уже будет недостаточно. Нужно, чтобы каждое событие могло произойти хотя бы несколько раз, а лучше - несколько десятков раз. Вы же упоминали такие малые значения, что ожидаемое число появлений события в серии меньше одного. Это значит, что для этой задачи длина серии слишком мала.

[orsobruno]

Цитата:

Это математически невозможно

Это если говорить об экстремумах. Но задача по оптимизация решаема. По крайней мере я для своих задач решение нашел.

Что касается погрешности генератора при малых значениях вероятностей, да это возможно, однако в моих экспериментах все значения встречаются. Погрешности также возможны при незначительном периоде прнг.

Цитата:

будет близко к математическому ожиданию только при большом числе опытов

Разумеется. Именно поэтому я подчеркнул что количество испытаний стремится к бесконечности.

Задача решена. Всем спасибо за помошь.