Вячеслав Овсейчик
О ЧИСЛАХ, КОТОРЫЕ ПРЕДПОЧИТАЕТ ПРИРОДА
1.Существует универсальная математическая модель нашего физического мира. Основу модели составляет специфическая функция, производные которой эквивалентны точкам бесконечной линии. Аргументом этой универсальной функции можно считать фазу. Поэтому линейные размеры объектов в таком пространстве могут иметь нулевую размерность.
Такой подход дает возможность выразить некоторые константы, имеющие размерность длины, через константы нулевой размерности.
Есть основание считать, что большую роль в формировании фундаментальных констант играют псевдочисла. Речь идет о характерных числах, рациональных и иррациональных, которые моделируются с помощью целых чисел. Для описания периодических процессов микромира может эффективно служить одно из псевдочисел ПИ:

Здесь


Здесь

- постоянная тонкой структуры электрона.
При использовании псевдочисла ПИ вместо числа ПИ в задаче Кеплера для системы, где внешняя частица вращается по эллипсу вокруг центральной частицы, как показывает анализ, появляются дополнительные степени свободы движения. Они возникают за счет отклонений псевдочисла от целого числа и могут быть отражены в разложении псевдочисла в бесконечную цепную дробь. Ясно, что природа не могла не воспользоваться такими возможностями в своей «практике». Не исключено, что пространственный масштаб - Бора радиус

образуется как безразмерный параметр на первичном уровне микромира и показывает некоторые детали взаимодействия числа

и псевдочисла

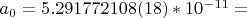
![$ = 1.000036929[17/(2\pi \alpha)]^4 $ $ = 1.000036929[17/(2\pi \alpha)]^4 $](https://dxdy-04.korotkov.co.uk/f/f/1/3/f139b1ac19c330674eee669f468363a682.png)
2. Число

достаточно часто появляется в константах, характеризующих периодические процессы и соотношения между периодическими последовательностями.
Замечено, что для волн на море (на глубокой воде) каждая девятая волна является самой сильной («девятый вал»). Реально, по–видимому, речь идет о параметре

, – каждая семнадцатая волна несет максимум. Но отсчет на практике ведут по полупериодам. При этом максимум обнаруживается после восьмой волны.
Одним из объяснений феномена

может быть тот факт, что при возникновении волновых структур для величин периодических промежутков отбираются наиболее короткие периодические последовательности наиболее простых (часто именно простых) чисел. Они являются наиболее устойчивыми.
Самая оригинальная из таких последовательностей связана с числом 17:

В центре находится число

, которое и определяет максимум пакета волн. В другую относительно крупную последовательность входит одно составное число:

Относительно устойчивой в мире относительно крупных волновых структур, по-видимому, будет та, которая имеет максимум

3. Итак, в мире элементарных частиц, видимо, не случайно встречается число

. Вели-чина отношения масс протона и электрона

может быть представлена как комбинация чисел:

Более точно отношение

может быть выражено с помощью чисел

Отметим, что параметр

появляется при пересчете величин из девятимерного стационарного пространства событий микромира в десятимерное нестационарное пространство.