Здравствуйте, помогите пожалуйста прояснить некоторые моменты в этой теореме.
Теорема:
Пусть дано поле
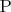
и неприводимый многочлен
![$ f \in \mathrm{P[x]}$ $ f \in \mathrm{P[x]}$](https://dxdy-04.korotkov.co.uk/f/3/7/b/37bbe0b966b1502f62df159634ee17cb82.png)
. Тогда существует расширение поля

в котором

имеет корень.
Докозательство:
Имеет смысл рассматривать подстановку в многочлен

над полем
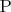
не элемента из поля
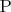
, а матрицы элементов из поля
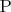
. В качестве матрицы, которую мы будем подставлять возьмём так называемую сопровождающую матрицу многочлена, изначально приняв

:

Рассмотрим строение выражения

. В частности заметим, что

,

,
...

.
Тогда


(1)
Аналогично

(2). Коммутативность была применена в силу того факта, что в выражении присутствуют степени одной и той же матрицы.
Рассмотри теперь всё множество всех матриц
![$\mathrm{A_f} =\left( g(A_f)|\forall g \in\mathrm{P[x]} \right)$ $\mathrm{A_f} =\left( g(A_f)|\forall g \in\mathrm{P[x]} \right)$](https://dxdy-04.korotkov.co.uk/f/3/1/6/31680834ce0151c4bc078d1f9dc99fb382.png)
. Это множество уже образует кольцо; корень многочлена

в этом кольце есть. Осталось показать что оно образует поле. Заметим, что в качестве многочленов

из
![$\mathrm{P[x]}$ $\mathrm{P[x]}$](https://dxdy-03.korotkov.co.uk/f/e/5/0/e50a38b7c6d8a87082fab30bf9dc1fd582.png)
мы можем рассматривать только те, чья степень строго меньше степени

. Действительно, если разделить

на

с остатком, имеем

,

.
Любой элемент из

представим в виде

, что соответствует некоторому многочлену из
![$\mathrm{P[x]}$ $\mathrm{P[x]}$](https://dxdy-03.korotkov.co.uk/f/e/5/0/e50a38b7c6d8a87082fab30bf9dc1fd582.png)
. Покажем, что если

, то

обратим в

. Так как

неприводим в
![$\mathrm{P[x]}$ $\mathrm{P[x]}$](https://dxdy-03.korotkov.co.uk/f/e/5/0/e50a38b7c6d8a87082fab30bf9dc1fd582.png)
, то

(3). Подставляя в эт равенство

получаем

. Так как

имеем

.
Доказано, что

- поле, в котором

имеет корень.
Итак, мы вводим новый элемент

.

это похоже что столбцы с нулевыми элементами, кроме элемента i который равен 1. Мы пользуемся этими столбцами, хотя они не входят ни в данное ни в расширенное поле. Они служат нам как вспомогательные элементы. И чтобы в конце концов доказать (1) нам требуются обычные операции умножения матрицы на эти столбцы и умножение элементов данного поля на столбцы. Мы считаем что в результате таких действий мы не придём к ложным заключениям. Нам даже не требуется определять операции между

и другими элементами множества, и операции между

и самим

. Тот ноль который мы получили в (1), это именно тот нулевой элемент из
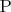
. Для (2) нам тоже ничего нового не требуется. Теперь, когда мы рассматриваем множество

всех матриц, мы говорим, что корень многочлена

в нём есть. Почему? Понятно что оно содержит и матрицу

и все элементы поля
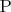
. Подразумевается что

тот самый корень. Т.е.

, но у нас пока есть только

. Наверно имеется ввиду, что если представить

как матрицу, то если хоть один элемент её не нулевой, то в одном из произведений

, что неверно. Или вообще тогда можно рассуждать так, что если

, то

что опять неверно, при этом непонятно зачем тогда вообще доказывать для других i. Итак

. Но при этом ноль, нулевой столбец и нулевая матрица отождествляются!! И к тому же, представляя

как матрицу нам уже пришлось бы вводить умножение элементов
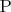
на

, сложение

которое очевидно определяется как

, где E - единичная матрица, а это уже получается второй единичный элемент в новом поле?! Ведь мы строим расширение поля, т.е. нам не просто нужно чтобы был гомоморфизм из
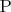
в

, а чтобы

включало
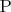
!! Это ведь разные вещи?!
В (3) мы конечно используем, что наибольший делитель

и

равен 1??
А затем мы опять получаем равенство с

. Причём если раньше быть может можно было сказать, что

используется как вспомогательный элемент для определения операций, то теперь он сам результат операции, т.е. должен принадлежать полю?!
Как видите много неясностей. Весь ход доказательства мне понятен, вот только эти неувязки портят всё впечатление. Может кто-нибудь разъяснить?