Вот натолкнулся на такой парадокс
Известно, что мощность континиуума равна
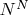
, где

-мощность счетного множества (в нашем случае множества натуральных чисел)
Так вот я построил биекцию между этими мощностями
Для начала преставим множество натуральных чиселкак бесконечно длинную последовательность кубиков- число которых бесконечно
А множество второе представим как мир- в котором счетное число измерений- и количество объектов в каждом измерении счетное (те
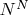
так вот- отформатируем для начала шкалу науральных чисел- закрасим число один в цвет номер один- число два и три в цвета номер один и два- числа четыре -пять-шесть в соответ цвета один-два-три и так далее
мы видим, что мы можем покрасить натуральные числа в бесконечное число цветов- и каждого цвета будет бесконеность(счетное количество)
так вот всем известно, что мощность

равна мощности

, где

-конечное число
так вот, значить, возьмем все натуральные числа с номером один (они покрашены в эту краску) и поставим во взаимно однозначное соответствие с первым измерением (прямой из кубиков) многомерного мира, теперь возьмем все числа с номером два- и поставим их во взаимооднозначное соответствие со вторым измерением многомерного мира (те плокостью из кубиков)
и так далее- каждой краски можно дать во взаимооднозначное соответствие количество измерений- совпадающей с номером этой краски
И тут мы видим- что число измерений счетно- и число различных красок счетно, и мы получили биекцию между
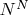
и

Что скажите?